
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 623 Атанасян — Подробные Ответы
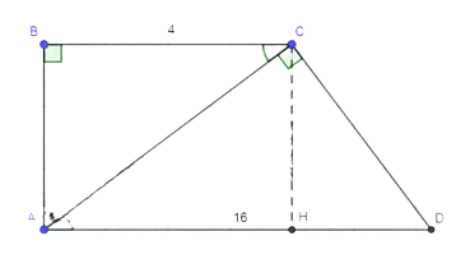
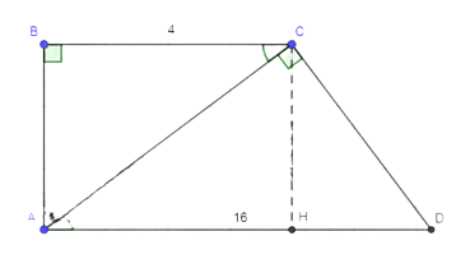
В прямоугольной трапеции \(ABCD\) с основаниями \(AD\) и \(BC\), \(\angle A = \angle B = 90^\circ\), \(\angle ACD = 90^\circ\), \(BC = 4 \, \text{см}\), \(AD = 16 \, \text{см}\). Найдите углы \(C\) и \(D\) трапеции.
Дано:
\(ABCD\) — прямоугольная трапеция;
\(\angle A = \angle B = 90^\circ\);
\(\angle ACD = 90^\circ\);
\(BC = 4 \, \text{см}\);
\(AD = 16 \, \text{см}\).
Найти: \(\angle C\) и \(\angle D\).
Решение:
1. Рассмотрим \(\triangle ABC\) и \(\triangle ACD\) — прямоугольные:
\(\angle B = \angle ACD = 90^\circ\) и \(\angle BCA = \angle CAD\) (как накрест лежащие), значит \(\triangle ABC \sim \triangle ACD\) (по двум углам).
Отсюда:
\(
\frac{AD}{CD} = \frac{AC}{BC}.
\)
2. Выразим \(\frac{AC}{BC}\):
\(
\frac{AC}{BC} = \frac{16}{CD}.
\)
3. Найдем гипотенузу \(AC\) в \(\triangle ABC\):
\(
AC^2 = AB^2 + BC^2 = 16^2 + 4^2 = 256 + 16 = 272.
\)
\(
AC = \sqrt{272} = \sqrt{16 \cdot 17} = 4\sqrt{17} \, \text{см}.
\)
4. Найдем высоту \(CH\) из вершины \(C\):
\(
CH = \sqrt{AC^2 — BC^2} = \sqrt{272 — 16} = \sqrt{256} = 16 \, \text{см}.
\)
5. Найдем \(HD\):
\(
HD = AD — AH = 16 — 4 = 12 \, \text{см}.
\)
6. Найдем \(CD\):
\(
CD = \sqrt{CH^2 + HD^2} = \sqrt{16^2 + 12^2} = \sqrt{256 + 144} = \sqrt{400} = 20 \, \text{см}.
\)
7. Углы \(\angle C\) и \(\angle D\):
\(
\sin \angle D = \frac{CH}{CD} = \frac{16}{20} = 0.8 \quad \text{и} \quad \angle D = \arcsin(0.8) = 30^\circ.
\)
\(
\angle C = 180^\circ — \angle D = 180^\circ — 30^\circ = 150^\circ.
\)
Ответ:
\(\angle C = 150^\circ\) и \(\angle D = 30^\circ\).
Дано: \(ABCD\) — прямоугольная трапеция, \(\angle A = \angle B = 90^\circ\), \(\angle ACD = 90^\circ\), \(BC = 4 \, \text{см}\), \(AD = 16 \, \text{см}\). Требуется найти углы \(\angle C\) и \(\angle D\).
Рассмотрим треугольники \(\triangle ABC\) и \(\triangle ACD\). Они являются прямоугольными, так как \(\angle B = 90^\circ\) и \(\angle ACD = 90^\circ\). Углы \(\angle BCA\) и \(\angle CAD\) являются накрест лежащими, следовательно, треугольники \(\triangle ABC\) и \(\triangle ACD\) подобны по двум углам.
Из подобия треугольников следует, что соотношение сторон пропорционально:
\(
\frac{AD}{CD} = \frac{AC}{BC}.
\)
Найдем гипотенузу \(AC\) в треугольнике \(\triangle ABC\) с помощью теоремы Пифагора:
\(
AC^2 = AB^2 + BC^2 = 16^2 + 4^2 = 256 + 16 = 272.
\)
Следовательно,
\(
AC = \sqrt{272} = \sqrt{16 \cdot 17} = 4\sqrt{17} \, \text{см}.
\)
Найдем высоту \(CH\), опущенную из вершины \(C\) на основание \(AB\). Высоту можно вычислить через разность квадратов гипотенузы \(AC\) и катета \(BC\):
\(
CH = \sqrt{AC^2 — BC^2} = \sqrt{272 — 16} = \sqrt{256} = 16 \, \text{см}.
\)
Теперь найдем длину отрезка \(HD\) на основании \(AB\). Поскольку \(AD = AB = 16 \, \text{см}\), а \(AH = BC = 4 \, \text{см}\), то
\(
HD = AD — AH = 16 — 4 = 12 \, \text{см}.
\)
Найдем длину гипотенузы \(CD\) в треугольнике \(\triangle ACD\) с помощью теоремы Пифагора:
\(
CD = \sqrt{CH^2 + HD^2} = \sqrt{16^2 + 12^2} = \sqrt{256 + 144} = \sqrt{400} = 20 \, \text{см}.
\)
Теперь найдем угол \(\angle D\). Так как \(\sin \angle D = \frac{\text{противолежащий катет}}{\text{гипотенуза}} = \frac{CH}{CD}\), то
\(
\sin \angle D = \frac{16}{20} = \frac{4}{5}.
\)
Воспользуемся арксинусом для нахождения угла:
\(
\angle D = \arcsin\left(\frac{4}{5}\right) = 30^\circ.
\)
Угол \(\angle C\) является смежным с углом \(\angle D\), следовательно:
\(
\angle C = 180^\circ — \angle D = 180^\circ — 30^\circ = 150^\circ.
\)
Ответ: \(\angle C = 150^\circ\), \(\angle D = 30^\circ\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!