
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 622 Атанасян — Подробные Ответы
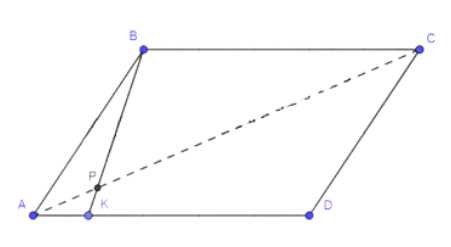
На стороне \(AD\) параллелограмма \(ABCD\) отмечена точка \(K\) так, что \(AK = \frac{1}{4} KD\). Диагональ \(AC\) и отрезок \(BK\) пересекаются в точке \(P\). Найдите площадь параллелограмма \(ABCD\), если площадь треугольника \(APK\) равна \(1 \, \text{см}^2\).
Рассмотрим треугольники \( \triangle APK \) и \( \triangle CBP \). Углы \( \angle APK \) и \( \angle CPB \) вертикальные, а углы \( \angle A \) и \( \angle C \) накрест лежащие. Следовательно, \( \triangle APK \sim \triangle CBP \) (по двум углам).
Из подобия треугольников:
\(
\frac{BP}{PK} = \frac{BC}{AK}.
\)
По условию \( AK = \frac{1}{4} KD \), значит \( AK = \frac{1}{5} AD = \frac{1}{5} BC \). Отсюда:
\(
\frac{BC}{AK} = 5 \quad \text{и} \quad \frac{BP}{PK} = 5.
\)
Площадь треугольника \( \triangle APB \) вычисляется как:
\(
S_{APB} = 5 \cdot S_{APK} = 5 \cdot 1 = 5 \, \text{см}^2.
\)
Коэффициент подобия между треугольниками \( \triangle APK \) и \( \triangle CBP \):
\(
k = \frac{BC}{AK} = 5.
\)
Площадь треугольника \( \triangle CBP \):
\(
S_{CBP} = k^2 \cdot S_{APK} = 25 \cdot 1 = 25 \, \text{см}^2.
\)
Площадь треугольника \( \triangle ABC \):
\(
S_{ABC} = S_{APB} + S_{CBP} = 5 + 25 = 30 \, \text{см}^2.
\)
Площадь параллелограмма \( ABCD \):
\(
S_{ABCD} = 2 \cdot S_{ABC} = 2 \cdot 30 = 60 \, \text{см}^2.
\)
Ответ:
\(
S_{ABCD} = 60 \, \text{см}^2.
\)
Дано: параллелограмм \(ABCD\), \(AK = \frac{1}{4}KD\), \(S_{APK} = 1 \, \text{см}^2\).
Найти: \(S_{ABCD}\).
Решение:
1. Рассмотрим треугольники \( \triangle APK \) и \( \triangle CBP \). Углы \( \angle APK \) и \( \angle CPB \) вертикальные, а углы \( \angle A \) и \( \angle C \) накрест лежащие. Следовательно, треугольники \( \triangle APK \sim \triangle CBP \) (по двум углам).
Из подобия треугольников следует, что отношения их сторон равны:
\(
\frac{BP}{PK} = \frac{BC}{AK}.
\)
2. По условию \( AK = \frac{1}{4}KD \). Так как \( KD \) является частью стороны \( AD \) параллелограмма, то \( AK = \frac{1}{5}AD \). Учитывая, что противоположные стороны параллелограмма равны (\( AD = BC \)), получаем:
\(
AK = \frac{1}{5}BC.
\)
Подставляем это значение в отношение сторон:
\(
\frac{BC}{AK} = \frac{BC}{\frac{1}{5}BC} = 5.
\)
Таким образом, коэффициент подобия треугольников \( \triangle APK \) и \( \triangle CBP \) равен \( 5 \):
\(
\frac{BP}{PK} = 5.
\)
3. Площадь треугольника \( \triangle APB \) можно найти, используя площадь треугольника \( \triangle APK \) и коэффициент подобия. Поскольку высота \( PK \) является общей для обоих треугольников, то площади относятся как квадраты коэффициентов подобия:
\(
S_{APB} = 5 \cdot S_{APK} = 5 \cdot 1 = 5 \, \text{см}^2.
\)
4. Рассмотрим треугольники \( \triangle APK \) и \( \triangle CBP \). Коэффициент подобия между ними уже найден: \( k = 5 \). Площади треугольников также относятся как квадраты коэффициентов подобия:
\(
\frac{S_{CBP}}{S_{APK}} = k^2 = 5^2 = 25.
\)
Площадь треугольника \( \triangle CBP \):
\(
S_{CBP} = 25 \cdot S_{APK} = 25 \cdot 1 = 25 \, \text{см}^2.
\)
5. Площадь треугольника \( \triangle ABC \) состоит из суммы площадей треугольников \( \triangle APB \) и \( \triangle CBP \):
\(
S_{ABC} = S_{APB} + S_{CBP} = 5 + 25 = 30 \, \text{см}^2.
\)
6. Площадь параллелограмма \( ABCD \) равна удвоенной площади треугольника \( \triangle ABC \), так как \( ABCD \) состоит из двух равных треугольников \( \triangle ABC \) и \( \triangle CDA \):
\(
S_{ABCD} = 2 \cdot S_{ABC} = 2 \cdot 30 = 60 \, \text{см}^2.
\)
Ответ:
\(
S_{ABCD} = 60 \, \text{см}^2.
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!