ГДЗ по Геометрии 8 класс Номер 618 Атанасян — Подробные Ответы

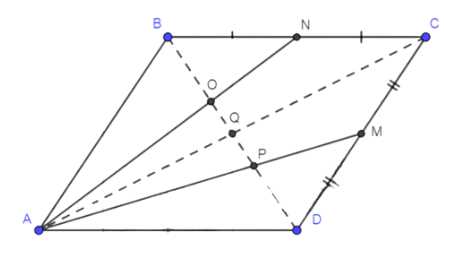
Точки \(M\) и \(N\) являются соответственно серединами сторон \(CD\) и \(BC\) параллелограмма \(ABCD\). Докажите, что прямые \(AM\) и \(AN\) делят диагональ \(BD\) на три равные части. 

Дано: \(ABCD\) — параллелограмм, \(BN = NC\), \(CM = MD\), \(N \in BC\), \(M \in CD\), \(AN \cap BD = O\), \(AM \cap BD = P\).
Доказать: \(BO = OP = PD\)

Решение:

1. Рассмотрим \(\triangle ABC\). \(AN\) и \(BQ\) — медианы, поэтому \(BO : OQ = 2 : 1\).
Из этого следует, что \(BO = \frac{2}{3}BQ\), а \(BQ = QD = \frac{1}{2}BD\).
Таким образом, \(BO = \frac{2}{3} \cdot \frac{1}{2}BD = \frac{1}{3}BD\).

2. Рассмотрим \(\triangle ACD\). \(AM\) и \(DQ\) — медианы, поэтому \(DP : PQ = 2 : 1\).
Из этого следует, что \(DP = \frac{2}{3}PQ\), а \(PQ = QD = \frac{1}{2}BD\).
Таким образом, \(DP = \frac{2}{3} \cdot \frac{1}{2}BD = \frac{1}{3}BD\).

3. \(OP = BD — BO — DP = BD — \frac{1}{3}BD — \frac{1}{3}BD = \frac{1}{3}BD\).

Следовательно, \(BO = OP = PD\).

Дано: \(ABCD\) — параллелограмм, \(BN = NC\), \(CM = MD\), \(N \in BC\), \(M \in CD\), \(AN \cap BD = O\), \(AM \cap BD = P\).
Доказать: \(BO = OP = PD\).

Решение:

1. Рассмотрим \(\triangle ABC\).
Поскольку \(N\) — середина \(BC\), а \(AN\) — медиана, то точка пересечения медиан \(O\) делит медиану \(AN\) в отношении \(2:1\), считая от вершины \(A\).
Аналогично, медиана \(BQ\) делится точкой \(O\) в отношении \(2:1\), считая от вершины \(B\).
Таким образом, \(BO : OQ = 2 : 1\).

2. Рассмотрим \(\triangle ACD\).
Поскольку \(M\) — середина \(CD\), а \(AM\) — медиана, то точка пересечения медиан \(P\) делит медиану \(AM\) в отношении \(2:1\), считая от вершины \(A\).
Аналогично, медиана \(DQ\) делится точкой \(P\) в отношении \(2:1\), считая от вершины \(D\).
Таким образом, \(DP : PQ = 2 : 1\).

3. Поскольку \(ABCD\) — параллелограмм, его диагонали \(AC\) и \(BD\) пересекаются в точке \(Q\), которая является их общей серединой. Следовательно, \(BQ = QD\).

4. Теперь выразим длины отрезков \(BO\), \(OQ\), \(DP\) и \(PQ\) через длину диагонали \(BD\).
Из пункта 1 мы знаем, что \(BO : OQ = 2 : 1\).
Обозначим длину диагонали \(BD\) через \(x\). Тогда \(BQ = QD = \frac{x}{2}\).
Поскольку \(BO = \frac{2}{3}BQ\), имеем:
\(
BO = \frac{2}{3} \cdot \frac{x}{2} = \frac{x}{3}.
\)

5. Аналогично, из пункта 2 мы знаем, что \(DP : PQ = 2 : 1\).
Поскольку \(DP = \frac{2}{3}PQ\), а \(PQ = QD = \frac{x}{2}\), имеем:
\(
DP = \frac{2}{3} \cdot \frac{x}{2} = \frac{x}{3}.
\)

6. Теперь найдём длину \(OP\).
Поскольку \(BD = BO + OQ + OP + PQ + DP\), имеем:
\(
OP = BD — BO — DP = x — \frac{x}{3} — \frac{x}{3} = x — \frac{2x}{3} = \frac{x}{3}.
\)

7. Таким образом, \(BO = OP = PD = \frac{x}{3}\).

Ответ: \(BO = OP = PD\).