
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 616 Атанасян — Подробные Ответы
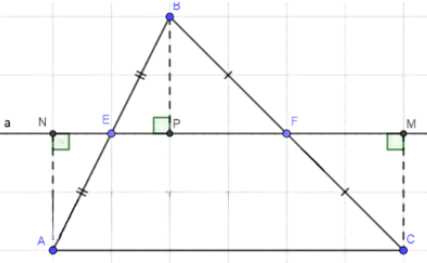
Докажите, что вершины треугольника равноудалены от прямой, содержащей его среднюю линию.
Дано:
\(
\Delta ABC, \quad a — \text{прямая}; \quad EF \parallel AC; \quad AN \perp a; \quad BP \perp a; \quad CM \perp a;\)
\(\quad EF \subset a;
\)
Доказать:
\(
BP = CM = AN.
\)
Доказательство:
1. Рассмотрим \(\Delta BPF\) и \(\Delta MFC\) — прямоугольные:
\(
BF = FC \quad (\text{по условию}), \quad \angle BFP = \angle MFC \quad (\text{как вертикальные}),
\)
значит, \(\Delta BPF \cong \Delta MFC\) (по гипотенузе и острому углу). Отсюда:
\(
BP = CM.
\)
2. Рассмотрим \(\Delta AEN\) и \(\Delta BPF\) — прямоугольные:
\(
EB = EA \quad (\text{по условию}), \quad \angle BEP = \angle NEA \quad (\text{как вертикальные}),
\)
значит, \(\Delta AEN \cong \Delta BPF\) (по гипотенузе и острому углу). Отсюда:
\(
AN = BP.
\)
3. \(
BP = CM \quad \text{и} \quad BP = AN, \quad \text{значит} \quad CM = AN = BP.
\)
Что и требовалось доказать.
Дано:
\(
\Delta ABC, \quad a — \text{прямая}; \quad EF \parallel AC; \quad AN \perp a; \quad BP \perp a; \quad CM \perp a;\)
\(\quad EF \subset a;
\)
Доказать:
\(
BP = CM = AN.
\)
Доказательство:
1. Рассмотрим треугольники \(\Delta BPF\) и \(\Delta MFC\).
Эти треугольники прямоугольные, так как \(BP \perp a\) и \(CM \perp a\).
По условию дано, что \(BF = FC\), а также углы \(\angle BFP\) и \(\angle MFC\) являются вертикальными:
\(
\angle BFP = \angle MFC.
\)
Следовательно, треугольники \(\Delta BPF\) и \(\Delta MFC\) равны по гипотенузе и острому углу.
Из равенства треугольников следует, что:
\(
BP = CM.
\)
2. Рассмотрим треугольники \(\Delta AEN\) и \(\Delta BPF\).
Эти треугольники также прямоугольные, так как \(AN \perp a\) и \(BP \perp a\).
По условию дано, что \(EB = EA\), а также углы \(\angle BEP\) и \(\angle NEA\) являются вертикальными:
\(
\angle BEP = \angle NEA.
\)
Следовательно, треугольники \(\Delta AEN\) и \(\Delta BPF\) равны по гипотенузе и острому углу.
Из равенства треугольников следует, что:
\(
AN = BP.
\)
3. Из пунктов 1 и 2 следует, что:
\(
BP = CM \quad \text{и} \quad BP = AN.
\)
Таким образом:
\(
CM = AN = BP.
\)
Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!