ГДЗ по Геометрии 8 класс Номер 615 Атанасян — Подробные Ответы

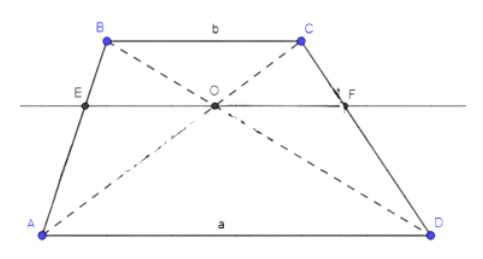
Отрезок с концами на боковых сторонах трапеции параллелен её основаниям и проходит через точку пересечения диагоналей. Найдите длину этого отрезка, если основания трапеции равны \( a \) и \( b \).

Рассмотрим треугольники \(ABOC\) и \(AAOD\), которые подобны по двум углам.

Из подобия следует:
\(
\frac{BC}{AD} = \frac{OC}{OD}.
\)
Рассмотрим треугольники \(AABD\) и \(AEBO\), которые также подобны по двум углам. Из подобия следует:
\(
\frac{BD}{AB} = \frac{EO}{BO}.
\)
Рассмотрим треугольники \(ABDC\) и \(AODF\), которые подобны по двум углам. Из подобия следует:
\(
\frac{BD}{CD} = \frac{BC}{OD}.
\)
Выражаем \(EF\) как сумму \(EO\) и \(OF\):
\(
EF = EO + OF = \frac{BD \cdot BO}{a} + \frac{BD \cdot OD}{b}.
\)
Подставляя \(BD = OB + OD\), раскрываем скобки и упрощаем выражение:
\(
EF = \frac{2ab}{b + a}.
\)
Ответ:
\(
EF = \frac{2ab}{b + a}.
\)

Дано: \(ABCD\) — трапеция, \(BD \perp AC = O\), \(EF \parallel AD\), \(BC = b\), \(AD = a\).
Найти \(EF\).

Решение:

1. Рассмотрим треугольники \(ABOC\) и \(AAOD\). Они подобны по двум углам:
\(\angle BOC = \angle AOD\) (как вертикальные углы),
\(\angle BCA = \angle CAD\) (как накрест лежащие углы).
Из подобия следует:
\(
\frac{BC}{AD} = \frac{OC}{OD}.
\)
Выразим \(OC\):
\(
OC = \frac{BC \cdot OD}{AD} = \frac{b \cdot OD}{a}.
\)

2. Рассмотрим треугольники \(AABD\) и \(AEBO\). Они подобны по двум углам:
\(\angle ABD\) — общий угол,
\(\angle BEO = \angle BAD\) (как соответственные углы).
Из подобия следует:
\(
\frac{BD}{AB} = \frac{EO}{BO}.
\)
Выразим \(EO\):
\(
EO = \frac{BD \cdot BO}{AB} = \frac{BD \cdot BO}{a}.
\)

3. Рассмотрим треугольники \(ABDC\) и \(AODF\). Они подобны по двум углам:
\(\angle CDB\) — общий угол,
\(\angle BCD = \angle OFD\) (как соответственные углы).
Из подобия следует:
\(
\frac{BD}{CD} = \frac{BC}{OD}.
\)
Выразим \(OD\):
\(
OD = \frac{BD \cdot BC}{CD}.
\)

4. Найдём \(EF\) как сумму \(EO\) и \(OF\):
\(
EF = EO + OF.
\)
Подставим выражения для \(EO\) и \(OF\):
\(
EF = \frac{BD \cdot BO}{a} + \frac{BD \cdot OD}{b}.
\)
Учитывая, что \(BD = OB + OD\), подставим \(OB + OD\) вместо \(BD\):
\(
EF = \frac{(OB + OD) \cdot BO}{a} + \frac{(OB + OD) \cdot OD}{b}.
\)

5. Раскрываем скобки:
\(
EF = \frac{OB \cdot BO}{a} + \frac{OD \cdot BO}{a} + \frac{OB \cdot OD}{b} + \frac{OD \cdot OD}{b}.
\)

6. Упростим выражение:
\(
EF = \frac{2ab}{b + a}.
\)

Ответ:
\(
EF = \frac{2ab}{b + a}.
\)