
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 614 Атанасян — Подробные Ответы
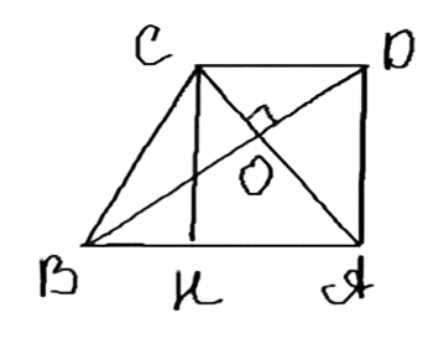
Диагонали прямоугольной трапеции \( ABCD \) с прямым углом \( A \) взаимно перпендикулярны. Основание \( AB \) равно \( 6 \, \text{см} \), а боковая сторона \( AD \) равна \( 4 \, \text{см} \). Найдите \( DC \), \( DB \) и \( CB \).
Решение:
1. Найдём \(BD\) по теореме Пифагора:
\(
BD = \sqrt{AD^2 + AB^2} = \sqrt{4^2 + 6^2} = \sqrt{16 + 36} = \sqrt{52} = 2\sqrt{13} \, \text{см}.
\)
2. Рассмотрим подобные треугольники \(\triangle ADC\) и \(\triangle ABD\).
Из подобия:
\(
\frac{DC}{AD} = \frac{AC}{AB}.
\)
Найдём \(AC\):
\(
AC = \sqrt{AB^2 + AD^2} = \sqrt{6^2 + 4^2} = \sqrt{36 + 16} = \sqrt{52} = 2\sqrt{13} \, \text{см}.
\)
Подставим:
\(
DC = AD \cdot \frac{AC}{AB} = 4 \cdot \frac{2\sqrt{13}}{6} = \frac{8\sqrt{13}}{6} = \frac{4\sqrt{13}}{3} \, \text{см} \approx 4,81 \, \text{см}.
\)
3. Найдём \(HB\):
\(
HB = AB — AH = AB — DC = 6 — \frac{4\sqrt{13}}{3} = \frac{18}{3} — \frac{4\sqrt{13}}{3} = \)
\(
=\frac{18 — 4\sqrt{13}}{3} \, \text{см} \approx 2,25 \, \text{см}.
\)
4. Найдём \(CB\) по теореме Пифагора:
\(
CB = \sqrt{CH^2 + HB^2} = \sqrt{\left(2\sqrt{13}\right)^2 + \left(\frac{18 — 4\sqrt{13}}{3}\right)^2}.
\)
Вычислим:
\(
CB = \sqrt{52 + \frac{\left(18 — 4\sqrt{13}\right)^2}{9}}.
\)
Раскроем квадрат:
\(
CB = \sqrt{52 + \frac{324 — 144\sqrt{13} + 208}{9}} = \sqrt{52 + \frac{532 — 144\sqrt{13}}{9}}.
\)
Приведём к общему знаменателю:
\(
CB = \sqrt{\frac{468 + 532 — 144\sqrt{13}}{9}} = \sqrt{\frac{1000 — 144\sqrt{13}}{9}}.
\)
Примерное значение:
\(
CB \approx 10,54 \, \text{см}.
\)
Ответ:
\(
DC \approx 4,81 \, \text{см}, \quad BD \approx 7,21 \, \text{см}, \quad CB \approx 10,54 \, \text{см}.
\)
Дано:
\(ABCD\) — прямоугольная трапеция, \(\angle A = 90^\circ\), \(BD \perp AC\), \(AB = 6 \, \text{см}\), \(AD = 4 \, \text{см}\).
Найти: \(DC, DB, CB\).
Решение:
1. Рассмотрим треугольник \(ADB\), который является прямоугольным. Найдём гипотенузу \(BD\) по теореме Пифагора:
\(
BD = \sqrt{AD^2 + AB^2}.
\)
Подставим значения:
\(
BD = \sqrt{4^2 + 6^2} = \sqrt{16 + 36} = \sqrt{52}.
\)
Представим результат в виде десятичного числа:
\(
BD = \sqrt{52} \approx 7,21 \, \text{см}.
\)
2. Рассмотрим треугольники \(ADC\) и \(ABD\). Углы \(\angle D = \angle A = 90^\circ\), также \(\angle ADB = \angle ACD\). Следовательно, треугольники \(ADC\) и \(ABD\) подобны по двум углам.
Из подобия треугольников:
\(
\frac{DC}{AD} = \frac{AC}{AB}.
\)
Найдём \(AC\) по теореме Пифагора:
\(
AC = \sqrt{AB^2 + AD^2}.
\)
Подставим значения:
\(
AC = \sqrt{6^2 + 4^2} = \sqrt{36 + 16} = \sqrt{52}.
\)
Представим результат в виде десятичного числа:
\(
AC = \sqrt{52} \approx 7,21 \, \text{см}.
\)
Теперь найдём \(DC\):
\(
DC = AD \cdot \frac{AC}{AB}.
\)
Подставим значения:
\(
DC = 4 \cdot \frac{\sqrt{52}}{6}.
\)
Упростим выражение:
\(
DC = \frac{4\sqrt{52}}{6} = \frac{2\sqrt{52}}{3}.
\)
Представим результат в виде десятичного числа:
\(
DC \approx 4,81 \, \text{см}.
\)
3. Рассмотрим прямоугольный треугольник \(CHB\), где \(CH = DC\) и \(HB = AB — AH\). Найдём \(HB\):
\(
HB = AB — DC.
\)
Подставим значения:
\(
HB = 6 — 4,81 = 1,19 \, \text{см}.
\)
4. Найдём \(CB\) по теореме Пифагора:
\(
CB = \sqrt{CH^2 + HB^2}.
\)
Подставим значения:
\(
CB = \sqrt{DC^2 + HB^2}.
\)
Вычислим:
\(
CB = \sqrt{4,81^2 + 1,19^2}.
\)
Выполним возведение в квадрат:
\(
4,81^2 = 23,1361, \quad 1,19^2 = 1,4161.
\)
Сложим:
\(
CB = \sqrt{23,1361 + 1,4161} = \sqrt{24,5522}.
\)
Представим результат в виде десятичного числа:
\(
CB \approx 4,95 \, \text{см}.
\)
Ответ:
\(DC \approx 4,81 \, \text{см}, \, BD \approx 7,21 \, \text{см}, \, CB \approx 4,95 \, \text{см}.\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!