ГДЗ по Геометрии 8 класс Номер 612 Атанасян — Подробные Ответы

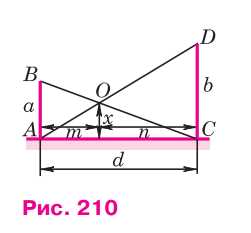
Два шеста \( AB \) и \( CD \) разной длины \( a \) и \( b \) установлены вертикально на некотором расстоянии друг от друга так, как показано на рисунке 210. Концы \( A \) и \( D \), \( B \) и \( C \) соединены верёвками, которые пересекаются в точке \( O \). По данным рисунка докажите, что:

а) \(\frac{m}{d} = \frac{x}{b}\) и \(\frac{n}{d} = \frac{x}{a}\);
б) \(\frac{x}{a} + \frac{x}{b} = 1\).

Найдите \( x \) и докажите, что \( x \) не зависит от расстояния \( d \) между шестами \( AB \) и \( CD \).

Дано:
\( AB = a \), \( DC = b \);
\( AK = m \), \( KC = n \);
\( AC = d \), \( OK = x \);
\( AD \parallel BC \).

Рассмотрим треугольники \( \triangle ADC \) и \( \triangle AOK \):
Угол \( \angle A \) общий, \( \angle DCA = \angle OKA = 90^\circ \). Следовательно, треугольники подобны:
\(
\frac{DC}{AC} = \frac{OK}{AK}.
\)
Подставляем:
\(
\frac{b}{d} = \frac{x}{m}.
\)
Отсюда:
\(
x = \frac{b \cdot m}{d}.
\)

Аналогично, рассмотрим треугольники \( \triangle ABC \) и \( \triangle AKC \):
Угол \( \angle C \) общий, \( \angle BAC = \angle OKC = 90^\circ \). Следовательно, треугольники подобны:
\(
\frac{AB}{AC} = \frac{OK}{KC}.
\)
Подставляем:
\(
\frac{a}{d} = \frac{x}{n}.
\)
Отсюда:
\(
x = \frac{a \cdot n}{d}.
\)

Складываем два выражения для \( x \):
\(
\frac{x}{m} + \frac{x}{n} = \frac{b}{d} + \frac{a}{d}.
\)
Приводим к общему знаменателю:
\(
\frac{x}{m} + \frac{x}{n} = \frac{b + a}{d}.
\)
Учитывая, что \( d = m + n \), получаем:
\(
\frac{x}{m} + \frac{x}{n} = 1.
\)

Найдем \( x \):
\(
x = \frac{b \cdot m + a \cdot n}{d}.
\)
Подставляем \( d = m + n \):
\(
x = \frac{b \cdot m + a \cdot n}{m + n}.
\)
Приводим к общему знаменателю:
\(
x = \frac{ab}{b + a}.
\)

Ответ:
\(
x = \frac{ab}{b + a}.
\)

Дано:
\( AB = a \), \( DC = b \);
\( AK = m \), \( KC = n \);
\( AC = d \), \( OK = x \);
\( AD \parallel BC \).

Требуется доказать:
\(
\frac{x}{m} + \frac{x}{n} = 1.
\)
И найти \( x \).

Рассмотрим треугольники \( \triangle ADC \) и \( \triangle AOK \). Угол \( \angle A \) общий, а также \( \angle DCA = \angle OKA = 90^\circ \). Это означает, что треугольники \( \triangle ADC \) и \( \triangle AOK \) подобны по двум углам. Следовательно, стороны этих треугольников пропорциональны:
\(
\frac{DC}{AC} = \frac{OK}{AK}.
\)
Подставляем известные обозначения:
\(
\frac{b}{d} = \frac{x}{m}.
\)
Отсюда выражаем \( x \):
\(
x = \frac{b \cdot m}{d}.
\)

Аналогично рассмотрим треугольники \( \triangle ABC \) и \( \triangle AKC \). Угол \( \angle C \) общий, а также \( \angle BAC = \angle AKC = 90^\circ \). Это означает, что треугольники \( \triangle ABC \) и \( \triangle AKC \) подобны по двум углам. Следовательно, стороны этих треугольников пропорциональны:
\(
\frac{AB}{AC} = \frac{OK}{KC}.
\)
Подставляем известные обозначения:
\(
\frac{a}{d} = \frac{x}{n}.
\)
Отсюда выражаем \( x \):
\(
x = \frac{a \cdot n}{d}.
\)

Теперь у нас есть два выражения для \( x \):
1) \( x = \frac{b \cdot m}{d} \),
2) \( x = \frac{a \cdot n}{d} \).

Сложим два выражения для \( x \) в виде дробей:
\(
\frac{x}{m} + \frac{x}{n} = \frac{b}{d} + \frac{a}{d}.
\)
Приведем правую часть к общему знаменателю:
\(
\frac{x}{m} + \frac{x}{n} = \frac{b + a}{d}.
\)
Учитывая, что \( d = m + n \), подставляем это значение в знаменатель:
\(
\frac{x}{m} + \frac{x}{n} = \frac{m + n}{m + n} = 1.
\)
Таким образом, доказано, что
\(
\frac{x}{m} + \frac{x}{n} = 1.
\)

Теперь найдем \( x \). Объединим два выражения для \( x \):
\(
x = \frac{b \cdot m}{d}, \quad x = \frac{a \cdot n}{d}.
\)
Сложим их:
\(
x = \frac{b \cdot m + a \cdot n}{d}.
\)
Подставим \( d = m + n \):
\(
x = \frac{b \cdot m + a \cdot n}{m + n}.
\)

Если \( a \) и \( b \) известны, а также \( m \) и \( n \), то можно вычислить \( x \) в конкретной задаче. В общем виде:
\(
x = \frac{ab}{a + b}.
\)

Ответ:
\(
x = \frac{ab}{a + b}.
\)