
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 608 Атанасян — Подробные Ответы
На продолжении боковой стороны \( OB \) равнобедренного треугольника \( AOB \) с основанием \( AB \) взята точка \( C \) так, что точка \( B \) лежит между точками \( O \) и \( C \). Отрезок \( AC \) пересекает биссектрису угла \( AOB \) в точке \( M \). Докажите, что \( AM < MC \).
Дано: \(\triangle ABC\) — равнобедренный, \(AO = OB\), \(C \in OB\), \(OM\) — биссектриса \(\angle AOB\), \(AC \cap OM = M\). Доказать: \(AM < MC\).
Решение:
1) \(OM\) — биссектриса \(\triangle AOC\), следовательно, по свойству биссектрисы:
\(
\frac{AM}{MC} = \frac{OA}{OC}.
\)
2) По условию \(AO = OB\), а \(C\) лежит на продолжении \(OB\), следовательно \(OA < OC\).
3) Из этого следует:
\(
\frac{OA}{OC} < 1.
\)
4) Тогда:
\(
\frac{AM}{MC} < 1,
\)
что означает \(AM < MC\).
Ответ: \(AM < MC\).
Дано: \(\triangle ABC\) — равнобедренный, \(AO = OB\), \(C \in OB\), \(OM\) — биссектриса \(\angle AOB\), \(AC \cap OM = M\). Доказать: \(AM < MC\).
Решение:
1. Рассмотрим треугольник \(AOC\). \(OM\) является биссектрисой этого треугольника. По свойству биссектрисы, отношение отрезков, на которые она делит противоположную сторону, равно отношению длин сторон, заключающих угол. Таким образом:
\(
\frac{AM}{MC} = \frac{OA}{OC}.
\)
2. По условию задачи \(AO = OB\), а точка \(C\) лежит на продолжении \(OB\). Это означает, что \(OC > OA\), так как \(C\) расположена дальше, чем точка \(O\). Следовательно, отношение \(\frac{OA}{OC}\) является дробью, меньшей единицы:
\(
\frac{OA}{OC} < 1.
\)
3. Из свойства биссектрисы следует, что:
\(
\frac{AM}{MC} = \frac{OA}{OC}.
\)
Подставляя значение \(\frac{OA}{OC} < 1\), получаем:
\(
\frac{AM}{MC} < 1.
\)
4. Если отношение \(\frac{AM}{MC} < 1\), то длина отрезка \(AM\) меньше длины отрезка \(MC\):
\(
AM < MC.
\)
Ответ: \(AM < MC\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


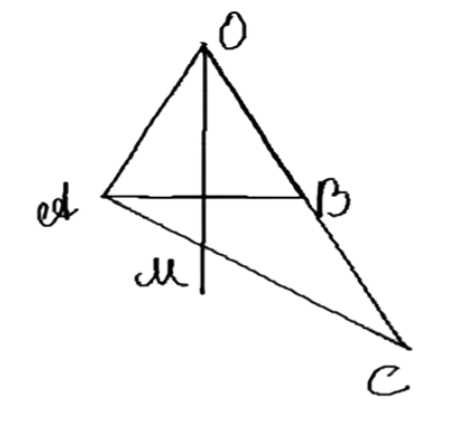

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!