
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 606 Атанасян — Подробные Ответы
Биссектрисы \( MD \) и \( NK \) треугольника \( MNP \) пересекаются в точке \( O \). Найдите отношение \( OK : ON \), если \( MN = 5 \, \text{см} \), \( NP = 3 \, \text{см} \), \( MP = 7 \, \text{см} \).
Дано:
\(\triangle MNP\);
\(MD\) и \(NK\) — биссектрисы;
\(MD \cap NK = O\);
\(MN = 5 \, \text{см}\);
\(NP = 3 \, \text{см}\);
\(MP = 7 \, \text{см}\).
Найти:
\(
\frac{OK}{ON} = ?
\)
Решение:
1) Пусть \(MK = x\), тогда \(KP = 7 — x \, \text{см}\).
2) Так как \(MK : KP = MN : NP\) (по задаче 535), то:
\(
\frac{MK}{KP} = \frac{MN}{NP}.
\)
Подставим значения:
\(
\frac{x}{7 — x} = \frac{5}{3}.
\)
Умножим крест-накрест:
\(
3x = (7 — x) \cdot 5.
\)
Раскроем скобки:
\(
3x = 35 — 5x.
\)
Перенесем \(5x\) в левую часть:
\(
3x + 5x = 35.
\)
Сложим:
\(
8x = 35.
\)
Найдем \(x\):
\(
x = \frac{35}{8} = 4 \frac{3}{8} \, \text{см}.
\)
3) Так как \(MO\) — биссектриса \(\triangle MKN\), то:
\(
\frac{OK}{ON} = \frac{MK}{MN}.
\)
Подставим значения:
\(
\frac{OK}{ON} = \frac{\frac{35}{8}}{5}.
\)
Преобразуем дробь:
\(
\frac{\frac{35}{8}}{5} = \frac{35}{8 \cdot 5} = \frac{35}{40} = \frac{7}{8}.
\)
Ответ:
\(
\frac{OK}{MN} = \frac{7}{8}.
\)
Дано: треугольник \( \triangle MNP \), биссектрисы \( MD \) и \( NK \), пересекающиеся в точке \( O \). Стороны треугольника имеют длины \( MN = 5 \, \text{см} \), \( NP = 3 \, \text{см} \), \( MP = 7 \, \text{см} \). Требуется найти отношение \( \frac{OK}{ON} \).
Решение:
1. Рассмотрим треугольник \( \triangle MNP \). Пусть \( MK = x \), тогда \( KP = 7 — x \), так как \( MP = 7 \, \text{см} \).
2. По свойству биссектрисы, проведенной из вершины \( N \), выполняется равенство:
\(
\frac{MK}{KP} = \frac{MN}{NP}.
\)
Подставляем известные значения:
\(
\frac{x}{7 — x} = \frac{5}{3}.
\)
3. Решим это уравнение. Умножим обе части на знаменатель \( 7 — x \):
\(
3x = 5(7 — x).
\)
Раскроем скобки:
\(
3x = 35 — 5x.
\)
Перенесем \( -5x \) в левую часть:
\(
3x + 5x = 35.
\)
Сложим:
\(
8x = 35.
\)
Найдем \( x \):
\(
x = \frac{35}{8} = 4 \frac{3}{8} \, \text{см}.
\)
4. Таким образом, \( MK = 4 \frac{3}{8} \, \text{см} \), а \( KP = 7 — x = 7 — 4 \frac{3}{8} = 2 \frac{5}{8} \, \text{см} \).
5. Теперь рассмотрим треугольник \( \triangle MKN \). В нём биссектриса \( MO \), проведённая из вершины \( M \), делит сторону \( NK \) на отрезки \( OK \) и \( ON \), пропорциональные прилежащим сторонам \( MK \) и \( MN \). По свойству биссектрисы:
\(
\frac{OK}{ON} = \frac{MK}{MN}.
\)
6. Подставим найденное значение \( MK = 4 \frac{3}{8} = \frac{35}{8} \) и \( MN = 5 \):
\(
\frac{OK}{ON} = \frac{\frac{35}{8}}{5}.
\)
Упростим дробь:
\(
\frac{\frac{35}{8}}{5} = \frac{35}{8 \cdot 5} = \frac{35}{40}.
\)
Сократим дробь:
\(
\frac{35}{40} = \frac{7}{8}.
\)
Ответ:
\(
\frac{OK}{ON} = \frac{7}{8}.
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


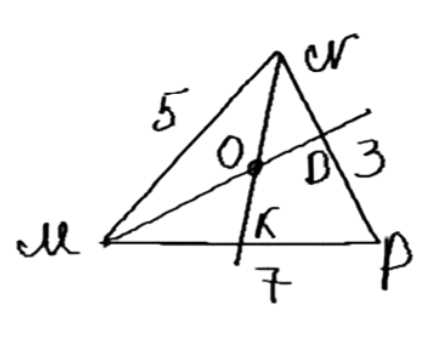

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!