
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 603 Атанасян — Подробные Ответы
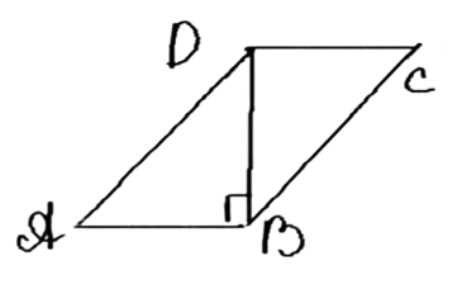
В параллелограмме \( ABCD \) сторона \( AD \) равна \( 12 \, \text{см} \), а угол \( BAD \) равен \( 47^\circ 50′ \). Найдите площадь параллелограмма, если его диагональ \( BD \) перпендикулярна к стороне \( AB \).
Дано: \(ABCD\) — параллелограмм, \(\angle BAD = 47^\circ 50’\), \(AD = 12 \, \text{см}\). Найти: \(S_{ABCD}\).
Решение:
Найдем диагональ \(BD\) и сторону \(AB\) через синус и косинус угла \(\angle BAD\):
\(
BD = AD \cdot \sin \angle BAD = 12 \cdot 0{,}7412 = 8{,}89 \, \text{см},
\)
\(
AB = AD \cdot \cos \angle BAD = 12 \cdot 0{,}6712 = 8{,}06 \, \text{см}.
\)
Площадь параллелограмма равна:
\(
S_{ABCD} = AB \cdot BD = 8{,}89 \cdot 8{,}06 = 71{,}76 \, \text{см}^2.
\)
Ответ: \(S_{ABCD} = 71{,}76 \, \text{см}^2\).
Дано:
\(ABCD\) — параллелограмм,
\(\angle BAD = 47^\circ 50’\),
\(AD = 12 \, \text{см}\),
\(BD\) — диагональ,
\(AB\) и \(BD\) — стороны.
Найти: \(S_{ABCD}\).
Решение:
1. Рассмотрим треугольник \(\triangle ABD\), который является прямоугольным.
В этом треугольнике сторона \(BD\) — это катет, противолежащий углу \(\angle BAD\), а сторона \(AB\) — это катет, прилежащий к углу \(\angle BAD\).
Найдем длину диагонали \(BD\) через синус угла \(\angle BAD\):
\(
BD = AD \cdot \sin \angle BAD = 12 \cdot \sin 47^\circ 50′.
\)
Подставим значение \(\sin 47^\circ 50′ = 0{,}7412\):
\(
BD = 12 \cdot 0{,}7412 = 8{,}89 \, \text{см}.
\)
Найдем длину стороны \(AB\) через косинус угла \(\angle BAD\):
\(
AB = AD \cdot \cos \angle BAD = 12 \cdot \cos 47^\circ 50′.
\)
Подставим значение \(\cos 47^\circ 50′ = 0{,}6712\):
\(
AB = 12 \cdot 0{,}6712 = 8{,}06 \, \text{см}.
\)
2. Площадь параллелограмма \(ABCD\) вычисляется по формуле:
\(
S_{ABCD} = AB \cdot BD.
\)
Подставим найденные значения \(AB = 8{,}06 \, \text{см}\) и \(BD = 8{,}89 \, \text{см}\):
\(
S_{ABCD} = 8{,}89 \cdot 8{,}06 = 71{,}7574 \, \text{см}^2.
\)
Округлим площадь до двух знаков после запятой:
\(
S_{ABCD} = 71{,}76 \, \text{см}^2.
\)
Ответ:
\(S_{ABCD} = 71{,}76 \, \text{см}^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!