
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 601 Атанасян — Подробные Ответы
Найдите углы ромба с диагоналями \( \frac{2\sqrt{3}}{3} \) и \( 2 \).
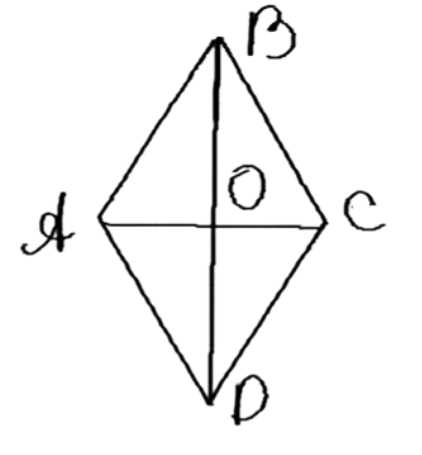
Дано: \(ABCD\) — ромб, \(AC = 2\), \(BD = 2\sqrt{3}\). Найти углы \(\angle A\) и \(\angle B\).
Решение:
1) В ромбе диагонали пересекаются под прямым углом и делятся пополам. Тогда:
\[
AO = OC = \frac{2}{2} = 1, \quad BO = OD = \frac{2\sqrt{3}}{2} = \sqrt{3}.
\]
2) В прямоугольном треугольнике \(\triangle ABO\):
\[
\tan \angle BAO = \frac{BO}{AO} = \frac{\sqrt{3}}{1} = \sqrt{3}.
\]
Отсюда \(\angle BAO = 60^\circ\).
3) \(\angle ABO = 90^\circ — \angle BAO = 90^\circ — 60^\circ = 30^\circ\).
4) Диагонали ромба являются биссектрисами его углов. Тогда:
\[
\angle A = 2 \cdot \angle BAO = 2 \cdot 60^\circ = 120^\circ,
\]
\[
\angle B = 2 \cdot \angle ABO = 2 \cdot 30^\circ = 60^\circ.
\]
Ответ: \(\angle A = 120^\circ, \, \angle B = 60^\circ\).
Дано: \(ABCD\) — ромб, \(AC = 2\), \(BD = 2\sqrt{3}\). Найти углы \(\angle A\) и \(\angle B\).
Решение:
1) По свойству ромба, его диагонали пересекаются под прямым углом и делятся пополам. Это означает, что точка пересечения диагоналей делит диагональ \(AC\) на две равные части, а также диагональ \(BD\) на две равные части. Таким образом:
\[
AO = OC = \frac{AC}{2} = \frac{2}{2} = 1,
\]
\[
BO = OD = \frac{BD}{2} = \frac{2\sqrt{3}}{2} = \sqrt{3}.
\]
2) Рассмотрим треугольник \(ABO\). Этот треугольник является прямоугольным (так как диагонали ромба пересекаются под прямым углом). В этом треугольнике катеты \(AO\) и \(BO\) известны:
\[
AO = 1, \quad BO = \sqrt{3}.
\]
Найдем угол \(\angle BAO\) с использованием тангенса:
\[
\tan \angle BAO = \frac{BO}{AO} = \frac{\sqrt{3}}{1} = \sqrt{3}.
\]
Из таблицы значений тригонометрических функций известно, что \(\tan 60^\circ = \sqrt{3}\). Следовательно,
\[
\angle BAO = 60^\circ.
\]
3) Угол \(\angle ABO\) в треугольнике \(ABO\) можно найти как разность между прямым углом и углом \(\angle BAO\):
\[
\angle ABO = 90^\circ — \angle BAO = 90^\circ — 60^\circ = 30^\circ.
\]
4) По свойству ромба, его диагонали являются биссектрисами углов. Это означает, что диагональ \(AC\) делит угол \(\angle A\) пополам, а диагональ \(BD\) делит угол \(\angle B\) пополам. Таким образом:
\[
\angle A = 2 \cdot \angle BAO = 2 \cdot 60^\circ = 120^\circ,
\]
\[
\angle B = 2 \cdot \angle ABO = 2 \cdot 30^\circ = 60^\circ.
\]
5) Углы ромба противоположны и равны, то есть \(\angle A = \angle C\), а \(\angle B = \angle D\). Поэтому:
\[
\angle A = \angle C = 120^\circ, \quad \angle B = \angle D = 60^\circ.
\]
Ответ: \(\angle A = 120^\circ, \, \angle B = 60^\circ\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!