
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 600 Атанасян — Подробные Ответы
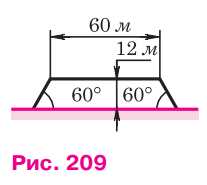
Насыпь шоссейной дороги имеет в верхней части ширину \( 60 \, \text{м} \). Какова ширина насыпи в нижней её части, если угол наклона откосов равен \( 60^\circ \), а высота насыпи равна \( 12 \, \text{м} \)?
Дано: \(ABCD\) — равнобедренная трапеция, \(\angle A = \angle D = 60^\circ\), \(AB = CD\), \(BH = 12\) м, \(BC = 60\) м. Найти \(AD\).
Решение:
1. Рассмотрим треугольники \(\triangle ABH\) и \(\triangle FCD\). Они равны, так как \(\angle A = \angle D\) и \(AB = CD\). Следовательно, \(AH = FD\).
2. Вычислим \(AH\):
\(
AH = \frac{BH}{\tan 60^\circ} = \frac{12}{\sqrt{3}} = 4\sqrt{3} \, \text{м}.
\)
3. Найдём \(AD\):
\(
AD = AH + HF + FD = 4\sqrt{3} + 60 + 4\sqrt{3} = 60 + 8\sqrt{3} \, \text{м}.
\)
4. Приближённое значение:
\(
AD \approx 73,84 \, \text{м}.
\)
Ответ: ширина насыпи \(73 \frac{21}{25}\) м или \(73,84\) м.
Дано:
\(ABCD\) — равнобедренная трапеция, \(\angle A = \angle D = 60^\circ\), \(AB = CD\), \(BH = 12\) м, \(BC = 60\) м. Найти \(AD\).
Решение:
1. По условию трапеция \(ABCD\) является равнобедренной. Следовательно, \(\angle A = \angle D = 60^\circ\), а также \(AB = CD\).
2. Рассмотрим треугольники \(\triangle ABH\) и \(\triangle FCD\). Эти треугольники прямоугольные, так как \(BH\) и \(FD\) — высоты трапеции. Кроме того, \(\triangle ABH = \triangle FCD\) по гипотенузе (\(AB = CD\)) и углу (\(\angle A = \angle D\)). Из равенства треугольников следует, что \(AH = FD\).
3. Вычислим длину \(AH\):
\(
AH = \frac{BH}{\tan 60^\circ}.
\)
Значение \(\tan 60^\circ = \sqrt{3}\), поэтому:
\(
AH = \frac{12}{\sqrt{3}} = 4\sqrt{3} \, \text{м}.
\)
4. Поскольку \(AH = FD\), длина основания \(AD\) трапеции определяется как:
\(
AD = AH + HF + FD.
\)
Подставим значения:
\(
AD = 4\sqrt{3} + 60 + 4\sqrt{3}.
\)
Сложим одинаковые слагаемые:
\(
AD = 60 + 8\sqrt{3} \, \text{м}.
\)
5. Выразим приближённое значение длины \(AD\). Приближённое значение \(\sqrt{3} \approx 1,732\):
\(
8\sqrt{3} \approx 8 \cdot 1,732 = 13,856.
\)
Тогда:
\(
AD \approx 60 + 13,856 = 73,856 \, \text{м}.
\)
Округлим до сотых:
\(
AD \approx 73,84 \, \text{м}.
\)
Ответ: ширина насыпи \(73 \frac{21}{25}\) м или \(73,84\) М.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!