
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 590 Атанасян — Подробные Ответы
Постройте прямоугольный треугольник по гипотенузе и отношению катетов, равному отношению двух данных отрезков.
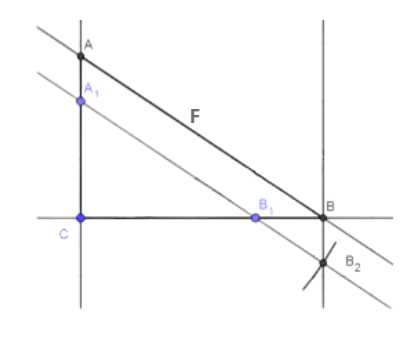
Построение прямоугольного треугольника \( \triangle ABC \), если \( \frac{CA}{CB} = \frac{a}{b} \):
1. Постройте прямой угол с вершиной в точке \( C \).
2. Отметьте на одной стороне угла отрезок \( CA = a \), а на другой стороне угла отрезок \( CB_1 = b \).
3. Проведите прямую \( A_1B_1 \) через точки \( A \) и \( B_1 \). На этой прямой отметьте отрезок \( A_1B_2 = AB \), равный гипотенузе треугольника.
4. Через точку \( B_2 \) проведите прямую, параллельную \( CA_1 \). На пересечении этой прямой с продолжением стороны \( CB \) отметьте точку \( B \).
5. Через точку \( B \) проведите прямую, параллельную \( A_1B_1 \). На пересечении этой прямой с продолжением стороны \( CA_1 \) отметьте точку \( A \).
6. Соедините точки \( A \), \( B \) и \( C \), чтобы получить треугольник \( \triangle ABC \).
Треугольник построен.
Построение прямоугольного треугольника \( \triangle ABC \), если \( \frac{CA}{CB} = \frac{a}{b} \), выполняется следующим образом:
1. Построим прямой угол с вершиной в точке \( C \). Для этого используем транспортир или угольник.
2. На одной стороне угла (например, горизонтальной) отложим отрезок \( CA \), равный \( a \). Для этого измерим длину \( a \) с помощью линейки или циркуля и отметим точку \( A \), такую что \( CA = a \).
3. На другой стороне угла (например, вертикальной) отложим отрезок \( CB_1 \), равный \( b \). Аналогично, измерим длину \( b \) и отметим точку \( B_1 \), такую что \( CB_1 = b \).
4. Проведем прямую \( A_1B_1 \), соединяющую точки \( A \) и \( B_1 \). Эта прямая является вспомогательной для дальнейшего построения.
5. На прямой \( A_1B_1 \) отметим точку \( B_2 \), такую что отрезок \( A_1B_2 \) равен гипотенузе \( AB \) треугольника. Длину гипотенузы \( AB \) можно вычислить заранее, используя пропорцию сторон \( \frac{CA}{CB} = \frac{a}{b} \) и теорему Пифагора:
\[
AB = \sqrt{a^2 + b^2}.
\]
Отложим эту длину на прямой \( A_1B_1 \) с помощью циркуля.
6. Через точку \( B_2 \) проведем прямую, параллельную стороне \( CA_1 \). Для этого используем угольник или линейку, чтобы обеспечить точность построения. Эта прямая пересечет продолжение стороны \( CB \) в точке \( B \).
7. Через точку \( B \) проведем прямую, параллельную стороне \( A_1B_1 \). Эта прямая пересечет продолжение стороны \( CA_1 \) в точке \( A \).
8. Соединим точки \( A \), \( B \) и \( C \) отрезками. Полученный треугольник \( \triangle ABC \) является прямоугольным, где \( \angle ACB = 90^\circ \), а отношение катетов \( \frac{CA}{CB} = \frac{a}{b} \).
9. Проверим построение. Убедимся, что:
— Угол \( \angle ACB \) прямой.
— Пропорция сторон \( \frac{CA}{CB} = \frac{a}{b} \) соблюдена.
— Длина гипотенузы \( AB \) соответствует вычисленному значению \( \sqrt{a^2 + b^2} \).
10. Построение завершено. Треугольник \( \triangle ABC \) соответствует заданным условиям.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!