
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 589 Атанасян — Подробные Ответы
Постройте треугольник \( ABC \) по углу \( A \) и стороне \( BC \), если известно, что \( AB : AC = 2 : 1 \).
Решение:
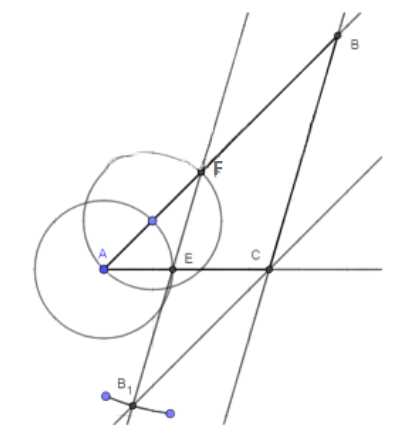
1. На одной стороне угла \(A\) отмечаем два равных отрезка произвольной длины \(AF = FE\), а на другой стороне угла один такой же отрезок \(AE\).
2. Отмечаем точки \(F\) и \(E\) на концах соответствующих отрезков.
3. Проводим прямую \(FE\). На этой прямой откладываем отрезок \(FB_1\), равный длине стороны \(BC\). Точка \(B_1\) — конец отрезка \(FB_1\).
4. Через точку \(B_1\) проводим прямую, параллельную \(AF\). На пересечении этой прямой с продолжением стороны \(AE\) отмечаем точку \(C\).
5. Через точку \(C\) проводим прямую, параллельную \(FE\). На пересечении этой прямой с продолжением стороны \(AF\) отмечаем точку \(B\).
6. Соединяем точки \(A\), \(B\) и \(C\), чтобы получить треугольник \(ABC\).
Треугольник построен по заданным углу и стороне \(BC\), при соблюдении пропорции \(AB : AC = 2 : 1\).
Решение:
1. На одной стороне угла \(A\) отмечаем два равных отрезка произвольной длины \(AF = FE\), а на другой стороне угла один такой же отрезок \(AE\). Для этого выбираем произвольную длину отрезка, например, \(l\), и с помощью циркуля откладываем два отрезка на одной стороне угла и один отрезок на другой стороне угла.
2. Отмечаем точки \(F\) и \(E\) на концах соответствующих отрезков. Точка \(F\) расположена на первой стороне угла, а точка \(E\) на второй стороне.
3. Проводим прямую \(FE\). На этой прямой откладываем отрезок \(FB_1\), равный длине стороны \(BC\). Для этого измеряем длину стороны \(BC\) циркулем или линейкой и откладываем её на прямой \(FE\), начиная от точки \(F\). Точка \(B_1\) — конец отрезка \(FB_1\).
4. Через точку \(B_1\) проводим прямую, параллельную \(AF\). Для построения параллельной прямой используем угольник или транспортир, чтобы обеспечить точное направление. На пересечении этой прямой с продолжением стороны \(AE\) отмечаем точку \(C\).
5. Через точку \(C\) проводим прямую, параллельную \(FE\). Для этого также используем угольник или транспортир, чтобы построить прямую, параллельную \(FE\). На пересечении этой прямой с продолжением стороны \(AF\) отмечаем точку \(B\).
6. Соединяем точки \(A\), \(B\) и \(C\), чтобы получить треугольник \(ABC\). Для этого используем линейку, чтобы провести отрезки \(AB\), \(AC\) и \(BC\).
7. Проверяем построение. Убедимся, что:
— Угол \(A\) соответствует заданному.
— Пропорция сторон \(AB : AC = 2 : 1\) соблюдена. Для этого измеряем длины сторон \(AB\) и \(AC\) линейкой и проверяем, что отношение их длин равно \(2 : 1\).
— Сторона \(BC\) соответствует заданной длине.
Треугольник \(ABC\) построен корректно в соответствии с заданными условиями.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!