
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 588 Атанасян — Подробные Ответы
Постройте треугольник \( ABC \) по углу \( A \) и медиане \( AM \), если известно, что \( AB : AC = 2 : 3 \).
Решение:
1. На одной стороне угла \(A\) отмечаем три равных отрезка любой длины, а на другой стороне — два таких же отрезка.
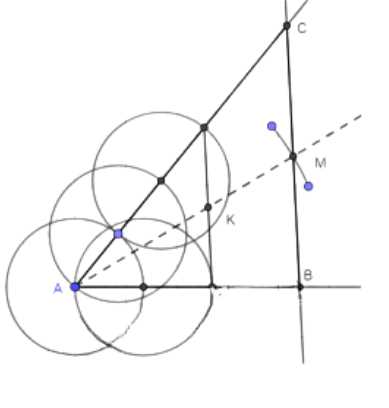
2. Проводим прямую через конец третьего отрезка на одной стороне и второго отрезка на другой стороне. На середине этой прямой отмечаем точку \(K\).
3. Проводим луч \(AK\) и на этом луче откладываем отрезок \(AM\), равный заданной медиане.
4. Через точку \(M\) проводим прямую, параллельную прямой из пункта 2.
5. На пересечении этой прямой с большей стороной угла отмечаем точку \(C\), а на пересечении с другой стороной угла — точку \(B\).
6. Соединяем точки \(A\), \(B\), \(C\).
Треугольник построен по заданным углу и медиане, с соблюдением пропорции сторон \(AB : AC = 2 : 3\).
Решение задачи:
Решение:
1. Начнем с построения угла \( \angle A \). Для этого чертим лучи \( AB \) и \( AC \), образующие заданный угол \( \angle A \).
2. На стороне \( AB \) откладываем три равных отрезка произвольной длины. Для этого выбираем любую длину отрезка, например, \( l \), и откладываем её три раза: \( AB_1 = B_1B_2 = B_2B_3 = l \). Точка \( B_3 \) — конец третьего отрезка.
3. На стороне \( AC \) откладываем два таких же отрезка длины \( l \): \( AC_1 = C_1C_2 = l \). Точка \( C_2 \) — конец второго отрезка.
4. Проводим прямую через точки \( B_3 \) и \( C_2 \). Эта прямая пересекает отрезок \( B_3C_2 \) в его середине. Обозначим эту середину как точку \( K \).
5. Проводим луч \( AK \). На этом луче откладываем отрезок \( AM \), равный заданной длине медианы. Для этого измеряем длину медианы циркулем или линейкой и откладываем её от точки \( A \) вдоль луча \( AK \). Точка \( M \) — конец отрезка \( AM \).
6. Через точку \( M \) проводим прямую, параллельную прямой \( B_3C_2 \). Для построения параллельной прямой используем угольник или транспортир, чтобы обеспечить точное направление.
7. Найдем точки пересечения этой прямой с продолжениями сторон угла \( \angle A \):
— Точка \( C \) — это точка пересечения прямой, проведенной через \( M \), с продолжением стороны \( AC \).
— Точка \( B \) — это точка пересечения прямой, проведенной через \( M \), с продолжением стороны \( AB \).
8. Соединяем точки \( A \), \( B \), \( C \), чтобы получить треугольник \( \triangle ABC \).
9. Проверяем построение:
— Угол \( \angle A \) соответствует заданному.
— Пропорция сторон \( AB : AC = 2 : 3 \) соблюдена, так как отрезки на сторонах \( AB \) и \( AC \) были отмечены в пропорции \( 2 : 3 \).
— Медиана \( AM \) равна заданной длине.
Треугольник \( \triangle ABC \) построен корректно в соответствии с заданными условиями.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!