Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
Ключевые особенности учебника:
1. Четкая структура:
Материал разбит на логически связанные разделы, каждый из которых посвящен отдельной теме, что облегчает восприятие и изучение.
2. Понятное изложение:
Доступный язык и стиль подачи материала делают даже сложные темы понятными для школьников.
3. Разнообразие задач:
Учебник содержит большое количество задач разной степени сложности, позволяя каждому ученику выбрать подходящие упражнения и совершенствовать свои навыки.
4. Наглядные иллюстрации:
Схемы и рисунки помогают лучше понять материал и визуализировать геометрические фигуры и их свойства.
5. Примеры из жизни:
Практические задачи, связанные с реальными ситуациями, делают изучение геометрии интересным и полезным.
6. Поддержка для учителей:
Методические рекомендации помогают преподавателям эффективно организовать уроки и использовать материал учебника.
Вывод:
Учебник Атанасяна по геометрии — это универсальный инструмент для изучения предмета, который сочетает понятность, практичность и разнообразие. Он подходит как для самостоятельного изучения, так и для работы в классе, делая процесс обучения более эффективным и увлекательным.
ГДЗ по Геометрии 8 класс Номер 587 Атанасян — Подробные Ответы
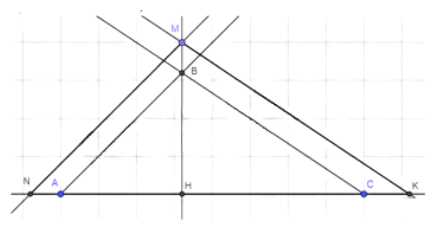
Постройте треугольник по двум углам и высоте, проведённой из вершины третьего угла.
1. Строим продолжение сторон большего угла. Для этого накладываем второй угол на одну из сторон первого угла и строим продолжение второй стороны. Обозначаем вершины угла как \(A\), \(B\), а точку пересечения сторон как \(C\).
2. Через точку \(B\) проводим перпендикуляр к прямой \(AC\). Этот перпендикуляр является высотой, проведённой из вершины \(B\).
3. На прямой \(AC\) отмечаем отрезок \(MH\), равный заданной высоте. Для этого откладываем длину высоты от точки \(M\) до точки \(H\) на прямой \(AC\).
4. Через точку \(M\) проводим прямые, параллельные сторонам \(AB\) и \(BC\). Это можно сделать с помощью угольника или линейки, обеспечивая строгое параллельное расположение.
5. На пересечении проведённых прямых с прямой \(AC\) отмечаем точки \(N\) и \(K\).
6. Соединяем точки \(A\), \(M\), \(N\), \(K\), чтобы получить искомый треугольник \(AMNK\).
Проверяем построение: угол \(A\) и угол \(B\) треугольника равны заданным углам, а высота, проведённая из вершины \(B\), равна заданной длине.
Решение задачи:
1. Начинаем построение с угла, большего из двух заданных углов. Для этого откладываем его на чертеже, используя транспортир. Обозначим вершину угла как \(C\), а стороны угла как \(CA\) и \(CB\). Продлеваем стороны угла \(CA\) и \(CB\) за пределы точки \(C\).
2. Затем накладываем второй заданный угол на одну из сторон первого угла \(CA\). Для этого используем транспортир, чтобы отложить второй угол на стороне \(CA\). Обозначим вершину второго угла как \(A\), а точку пересечения сторон второго угла с продолжением стороны \(CB\) обозначим как \(B\). Таким образом, получаем треугольник \(ABC\), в котором известны два угла.
3. Через точку \(B\) проводим перпендикуляр к прямой \(AC\). Для этого используем угольник или транспортир, чтобы провести прямую, перпендикулярную \(AC\), через точку \(B\). Этот перпендикуляр является высотой треугольника, проведённой из вершины \(B\).
4. На прямой \(AC\) отмечаем отрезок \(MH\), равный заданной высоте. Для этого измеряем длину высоты циркулем или линейкой, откладываем её на прямой \(AC\) от точки \(M\) до точки \(H\). Точка \(M\) лежит на прямой \(AC\), а точка \(H\) лежит на перпендикуляре, проведённом через \(B\).
5. Через точку \(M\) проводим две прямые, параллельные сторонам \(AB\) и \(BC\). Для построения параллельных прямых используем угольник или линейку, чтобы обеспечить строгое параллельное расположение. Параллельная сторона \(AB\) пересекает прямую \(AC\) в точке \(N\), а параллельная сторона \(BC\) пересекает прямую \(AC\) в точке \(K\).
6. Обозначаем точки пересечения: \(N\) — точка пересечения параллели к \(AB\) с прямой \(AC\), \(K\) — точка пересечения параллели к \(BC\) с прямой \(AC\).
7. Соединяем точки \(A\), \(M\), \(N\), \(K\), чтобы получить искомый треугольник \(AMNK\). Проверяем соответствие условиям задачи:
— Угол \(A\) треугольника равен первому заданному углу.
— Угол \(B\) треугольника равен второму заданному углу.
— Высота, проведённая из вершины \(B\), равна заданной длине.
Построение выполнено корректно, так как все шаги соответствуют правилам геометрии, а треугольник \(AMNK\) удовлетворяет всем условиям задачи.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.