ГДЗ по Геометрии 8 класс Номер 586 Атанасян — Подробные Ответы

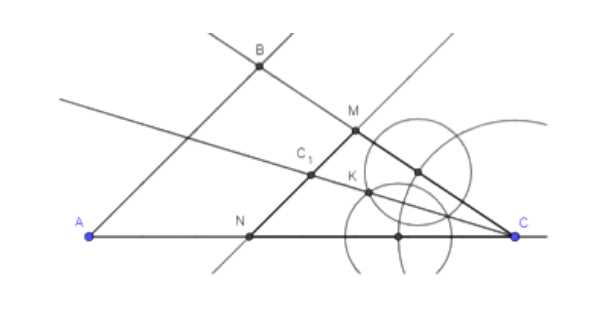
Постройте треугольник по двум углам и биссектрисе, проведённой из вершины меньшего из данных углов.

1. Строим продолжения сторон большего угла, накладываем второй угол на сторону первого и также строим продолжение второй стороны. Получаем пересечение этих сторон в точке \(C\).
2. На углах отмечаем точки \(A\) и \(B\), а точка пересечения сторон — это точка \(C\).
3. Внутри угла \(C\) отмечаем точку, которая делит угол пополам, и проводим через неё луч \(CK\), являющийся биссектрисой.
4. На луче \(CK\) отмечаем отрезок \(CC_1\), равный длине биссектрисы, заданной в условии.
5. Через точку \(C_1\) проводим прямую, параллельную стороне \(AB\), и на пересечении этой прямой со сторонами угла \(C\) отмечаем точки \(M\) и \(N\).
6. Треугольник \(AMNC\) является искомым.

1. Строим продолжения сторон большего угла. Для этого откладываем заданный угол на стороне первого и строим продолжение второй стороны. Пусть вершины угла обозначены как \(A\) и \(B\), а точка пересечения сторон — как \(C\).

2. Отмечаем на чертеже точки \(A\) и \(B\), а также точку пересечения \(C\). Таким образом, получаем треугольник, в котором угол \(C\) является заданным.

3. Внутри угла \(C\) отмечаем точку, которая делит угол пополам. Для этого используем метод построения биссектрисы:
— Берём циркуль и проводим дугу из вершины \(C\), которая пересекает обе стороны угла. Пусть точки пересечения дуги со сторонами угла обозначены как \(D\) и \(E\).
— Из точек \(D\) и \(E\) проводим дуги одинакового радиуса, которые пересекаются в точке \(K\).
— Соединяем точку \(C\) с точкой \(K\). Полученный луч \(CK\) является биссектрисой угла \(C\).

4. На биссектрисе \(CK\) отмечаем отрезок \(CC_1\), равный длине заданной биссектрисы. Для этого откладываем равный отрезок с помощью циркуля или линейки.

5. Через точку \(C_1\) проводим прямую, параллельную стороне \(AB\). Для построения параллельной прямой:
— Используем угольник или транспортир, чтобы провести прямую через точку \(C_1\), параллельную стороне \(AB\).

6. На пересечении этой прямой со сторонами угла \(C\) отмечаем точки \(M\) и \(N\). Для этого:
— Находим пересечение прямой, проведённой через \(C_1\), с продолжением стороны \(AC\) и стороны \(BC\).
— Обозначаем точки пересечения как \(M\) и \(N\).

7. Треугольник \(AMNC\) является искомым. Проверяем его соответствие условию задачи:
— Угол \(C\) треугольника равен заданному углу.
— Биссектриса угла \(C\) равна заданной длине.
— Построение выполнено корректно, так как все шаги соответствуют правилам геометрии.