
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 584 Атанасян — Подробные Ответы
Разделите данный отрезок \(AB\) на два отрезка \(AX\) и \(XB\), пропорциональные данным отрезкам \(P_1Q_1\) и \(P_2Q_2\).
Решение
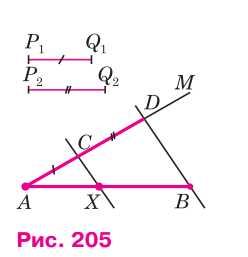
Проведём какой-нибудь луч \(AM\), не лежащий на прямой \(AB\), и на этом луче отложим последовательно отрезки \(AC\) и \(CD\), равные отрезкам \(P_1Q_1\) и \(P_2Q_2\) (рис. 205). Затем проведём прямую \(BD\) и прямую, проходящую через точку \(C\) параллельно прямой \(BD\). Она пересечёт отрезок \(AB\) в искомой точке \(X\) (см. задачу 556).
Решение задачи заключается в следующем:
1. Построим произвольный луч \(AM\).
2. На данном луче последовательно отложим отрезки \(AC\) и \(CD\), длины которых равны \(P_1Q_1\) и \(P_2Q_2\) соответственно.
3. Через точку \(C\) проведем прямую, параллельную \(BD\).
4. На пересечении этой прямой с отрезком \(AB\) отметим точку \(X\).
Таким образом, точка \(X\) делит отрезок \(AB\) на части \(AX\) и \(XB\), пропорциональные \(P_1Q_1\) и \(P_2Q_2\).
Рассмотрим задачу о делении отрезка \(AB\) на два отрезка \(AX\) и \(XB\), пропорциональные заданным отрезкам \(P_1Q_1\) и \(P_2Q_2\). Выполним решение с подробным описанием всех шагов.
Дано:
Отрезок \(AB\). Требуется найти точку \(X\) на этом отрезке, чтобы выполнялось соотношение:
\[
\frac{AX}{XB} = \frac{P_1Q_1}{P_2Q_2}.
\]
Решение:
1. Построим произвольный луч \(AM\), который не лежит на прямой \(AB\). Это луч используется для откладывания заданных отрезков.
2. На луче \(AM\) последовательно отложим два отрезка:
\(AC = P_1Q_1\) и \(CD = P_2Q_2\).
То есть длина отрезка \(AC\) равна длине \(P_1Q_1\), а длина отрезка \(CD\) равна длине \(P_2Q_2\). Точка \(C\) будет концом первого отрезка, а точка \(D\) концом второго отрезка.
3. Соединим точку \(B\) с точкой \(D\), проведя прямую \(BD\).
4. Через точку \(C\) проведем прямую, параллельную прямой \(BD\). Для этого используется свойство параллельных прямых: через точку \(C\) можно провести единственную прямую, параллельную \(BD\). Эта прямая пересечет отрезок \(AB\) в некоторой точке \(X\).
5. Точка \(X\) является искомой точкой, которая делит отрезок \(AB\) на два отрезка \(AX\) и \(XB\), пропорциональные \(P_1Q_1\) и \(P_2Q_2\). То есть выполняется равенство:
\[
\frac{AX}{XB} = \frac{P_1Q_1}{P_2Q_2}.
\]
Обоснование правильности метода:
Построение основано на свойстве подобия треугольников. Треугольники \(ACX\) и \(BDX\) подобны, так как их стороны пропорциональны (по построению), а углы равны (соответствующие углы равны, так как прямые \(CX\) и \(BD\) параллельны). Это обеспечивает выполнение условия пропорциональности.
Ответ: точка \(X\) на отрезке \(AB\) делит его на части \(AX\) и \(XB\), пропорциональные отрезкам \(P_1Q_1\) и \(P_2Q_2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!