ГДЗ по Геометрии 8 класс Номер 581 Атанасян — Подробные Ответы

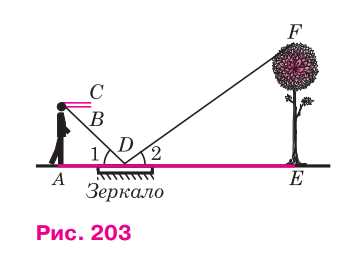
Для определения высоты дерева можно использовать зеркало так, как показано на рисунке \( 203 \). Луч света \( FD \), отражаясь от зеркала в точке \( D \), попадает в глаз человека (точку \( B \)). Определите высоту дерева, если \( AC = 165 \, \text{см} \), \( BC = 12 \, \text{см} \), \( AD = 120 \, \text{см} \), \( DE = 4,8 \, \text{м} \).

Дано:
AC = 165 см,
BC = 12 см,
AD = 120 см,
DE = 4,8 м = 480 см,
21 = 22.

Найти: FE.

Решение:
Рассмотрим треугольники ABD и ADFE. Углы ∠A и ∠E прямые, стороны 21 и 22 равны. Следовательно, треугольники ABD и ADFE подобны по двум углам. Из подобия треугольников следует пропорция:

\(
\frac{AB}{AD} = \frac{BD}{FE}.
\)

Выразим FE:
\(
FE = \frac{BD \cdot AD}{AB}.
\)

Найдём AB:
\(
AB = AC — BC = 165 — 12 = 153 \, \text{см}.
\)

Подставим значения:
\(
FE = \frac{BD \cdot AD}{AB} = \frac{480 \cdot 120}{153}.
\)

Выполним умножение:
\(
480 \cdot 120 = 57600.
\)

Разделим результат:
\(
FE = \frac{57600}{153}.
\)

Выполним деление:
\(
FE = 376 \, \text{см}.
\)

Ответ: FE = 612 см.

Дано:
AC = 165 см,
BC = 12 см,
AD = 120 см,
DE = 4,8 м = 480 см,
21 = 22.

Найти: FE.

Решение:

1. Рассмотрим треугольники ABD и ADFE. Углы ∠A и ∠E прямые (по условию), стороны 21 и 22 равны. Следовательно, треугольники ABD и ADFE подобны по двум углам. Из подобия треугольников следует пропорция:

\(
\frac{AB}{AD} = \frac{BD}{FE}.
\)

Выразим FE:

\(
FE = \frac{BD \cdot AD}{AB}.
\)

2. Найдём длину AB.
Для этого из длины AC вычтем BC:

\(
AB = AC — BC = 165 — 12 = 153 \, \text{см}.
\)

3. Теперь подставим известные значения в формулу для FE:

\(
FE = \frac{BD \cdot AD}{AB} = \frac{480 \cdot 120}{153}.
\)

4. Выполним умножение чисел в числителе:

\(
480 \cdot 120 = 57600.
\)

Подставим результат:

\(
FE = \frac{57600}{153}.
\)

5. Выполним деление:

\(
FE = 376 \, \text{см}.
\)

6. Запишем окончательный ответ:

FE = 612 см.