
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 578 Атанасян — Подробные Ответы
Используя утверждение \( 2^\circ \), п. 65, докажите теорему Пифагора: в прямоугольном треугольнике \( \triangle ABC \) с прямым углом \( C \) выполняется равенство
\(
AC^2 + BC^2 = AB^2.
\)
Решение
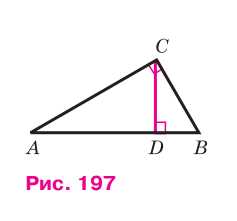
Пусть \( CD \) — высота треугольника \( \triangle ABC \) (см. рис. 197). На основании утверждения \( 2^\circ \), п. 65, имеем
\(
AC = \sqrt{AD \cdot AB}, \quad \text{или} \quad AC^2 = AD \cdot AB.
\)
Аналогично
\(
BC^2 = BD \cdot AB.
\)
Складывая эти равенства почленно и учитывая, что \( AD + BD = AB \), получаем:
\(
AC^2 + BC^2 = AD \cdot AB + BD \cdot AB = (AD + BD) \cdot AB = AB^2.
\)
Дано: треугольник \( \triangle ABC \), прямоугольный (\( \angle C = 90^\circ \)), высота \( CD \perp AB \), \( AC = \sqrt{AB \cdot AD} \), \( BC = \sqrt{AB \cdot BD} \). Требуется доказать, что \( AC^2 + BC^2 = AB^2 \).
Решение:
1. Пусть \( CD \) — высота треугольника \( \triangle ABC \). По условию:
\(
AC = \sqrt{AB \cdot AD}, \quad BC = \sqrt{AB \cdot BD}.
\)
2. Возведем обе стороны в квадрат:
\(
AC^2 = AB \cdot AD, \quad BC^2 = AB \cdot BD.
\)
3. Запишем сумму квадратов:
\(
AC^2 + BC^2 = AB \cdot AD + AB \cdot BD.
\)
4. Вынесем \( AB \) за скобки:
\(
AC^2 + BC^2 = AB \cdot (AD + BD).
\)
5. Так как \( AD + BD = AB \), то:
\(
AC^2 + BC^2 = AB \cdot AB = AB^2.
\)
Доказано, что \( AC^2 + BC^2 = AB^2 \).
Дано: треугольник \( \triangle ABC \), прямоугольный (\( \angle C = 90^\circ \)), высота \( CD \perp AB \), \( AC = \sqrt{AB \cdot AD} \), \( BC = \sqrt{AB \cdot BD} \). Требуется доказать, что \( AC^2 + BC^2 = AB^2 \).
Решение:
1. Рассмотрим прямоугольный треугольник \( \triangle ABC \), в котором высота \( CD \) проведена перпендикулярно гипотенузе \( AB \). По свойству прямоугольного треугольника, высота делит гипотенузу \( AB \) на два отрезка: \( AD \) и \( BD \), таких что:
\(
AB = AD + BD.
\)
2. Согласно условию задачи, для катетов \( AC \) и \( BC \) выполняются следующие равенства:
\(
AC = \sqrt{AB \cdot AD}, \quad BC = \sqrt{AB \cdot BD}.
\)
3. Возведем обе стороны этих равенств в квадрат:
\(
AC^2 = AB \cdot AD, \quad BC^2 = AB \cdot BD.
\)
4. Найдем сумму квадратов катетов:
\(
AC^2 + BC^2 = AB \cdot AD + AB \cdot BD.
\)
5. Вынесем \( AB \) за скобки:
\(
AC^2 + BC^2 = AB \cdot (AD + BD).
\)
6. Учитывая, что \( AD + BD = AB \) (по определению гипотенузы), получаем:
\(
AC^2 + BC^2 = AB \cdot AB.
\)
7. Следовательно:
\(
AC^2 + BC^2 = AB^2.
\)
Таким образом, доказано, что сумма квадратов катетов в прямоугольном треугольнике равна квадрату гипотенузы, что соответствует теореме Пифагора.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!