
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 568 Атанасян — Подробные Ответы
Докажите, что четырёхугольник — ромб, если его вершинами являются середины сторон:
а) прямоугольника;
б) равнобедренной трапеции.
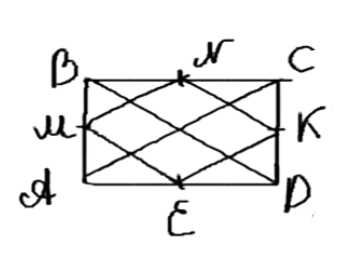
Дано:
ABCD — прямоугольник,
AM = MB, BN = NC, CK = KD, AE = ED.
Доказать: MNKE — ромб.
Решение:
1. Рассмотрим треугольник \(\triangle ABD\):
AM = MB (по условию), AE = ED (по условию).
ME — средняя линия (по определению).
По теореме о средней линии:
\(ME = \frac{1}{2}BD.\)
2. Рассмотрим треугольник \(\triangle BCD\):
BN = NC (по условию), CK = KD (по условию).
NK — средняя линия (по определению).
По теореме о средней линии:
\(NK = \frac{1}{2}BD.\)
3. Рассмотрим треугольник \(\triangle ABC\):
AM = MB (по условию), BN = NC (по условию).
MN — средняя линия (по определению).
По теореме о средней линии:
\(MN = \frac{1}{2}AC.\)
4. Рассмотрим треугольник \(\triangle ADC\):
AE = ED (по условию), CK = KD (по условию).
KE — средняя линия (по определению).
По теореме о средней линии:
\(KE = \frac{1}{2}AC.\)
5. MN \(\parallel\) AC и KE \(\parallel\) AC, следовательно, MN \(\parallel\) KE.
6. ME \(\parallel\) BD и NK \(\parallel\) BD, следовательно, ME \(\parallel\) NK.
7. Так как ABCD — прямоугольник, то:
\(ME = NK = MN = KE.\)
8. MN \(\parallel\) KE, ME \(\parallel\) NK, следовательно, MNKE — параллелограмм.
Кроме того, \(ME = NK = MN = KE,\) значит, MNKE — ромб (по определению).
Что и требовалось доказать.
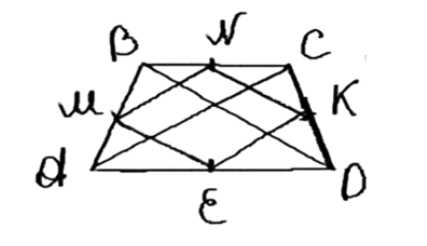
б)
Дано: ABCD — прямоугольник.
AM = MB, BN = NC, CK = KD, AE = ED.
Доказать: MNKE — ромб.
Решение:
1. Рассмотрим треугольник ABD.
AM = MB и AE = ED (по условию), следовательно, ME — средняя линия.
По теореме о средней линии:
ME = ½ BD.
2. Рассмотрим треугольник BCD.
BN = NC и CK = KD (по условию), следовательно, NK — средняя линия.
По теореме о средней линии:
NK = ½ BD.
3. Рассмотрим треугольник ABC.
AM = MB и BN = NC (по условию), следовательно, MN — средняя линия.
По теореме о средней линии:
MN = ½ AC.
4. Рассмотрим треугольник ADC.
AE = ED и CK = KD (по условию), следовательно, KE — средняя линия.
По теореме о средней линии:
KE = ½ AC.
5. MN параллельно AC, KE параллельно AC, следовательно, MN параллельно KE.
6. ME параллельно BD, NK параллельно BD, следовательно, ME параллельно NK.
7. Диагонали прямоугольника равны, значит:
ME = NK = MN = KE.
8. MN параллельно KE, ME параллельно NK, а также ME = NK = MN = KE, следовательно, MNKE — параллелограмм с равными сторонами.
Таким образом, MNKE — ромб.
Что и требовалось доказать.
а) Дано: ABCD — прямоугольник, AM = MB, BN = NC, CK = KD, AE = ED.
Доказать: MNKE — ромб.
Решение:
1. Рассмотрим треугольник ABD.
AM = MB (по условию), AE = ED (по условию).
ME — средняя линия треугольника ABD (по определению средней линии).
Согласно теореме о средней линии, средняя линия треугольника равна половине основания:
ME = ½ BD.
2. Рассмотрим треугольник BCD.
BN = NC (по условию), CK = KD (по условию).
NK — средняя линия треугольника BCD (по определению средней линии).
Согласно теореме о средней линии:
NK = ½ BD.
3. Рассмотрим треугольник ABC.
AM = MB (по условию), BN = NC (по условию).
MN — средняя линия треугольника ABC (по определению средней линии).
Согласно теореме о средней линии:
MN = ½ AC.
4. Рассмотрим треугольник ADC.
AE = ED (по условию), CK = KD (по условию).
KE — средняя линия треугольника ADC (по определению средней линии).
Согласно теореме о средней линии:
KE = ½ AC.
5. Поскольку MN параллельно AC и KE параллельно AC (по построению средних линий), то MN параллельно KE.
6. Поскольку ME параллельно BD и NK параллельно BD (по построению средних линий), то ME параллельно NK.
7. Поскольку ABCD — прямоугольник, то его диагонали равны и делятся пополам. Следовательно:
ME = NK = MN = KE.
8. MN параллельно KE, ME параллельно NK, а также ME = NK = MN = KE.
Таким образом, MNKE — параллелограмм, у которого все стороны равны.
Согласно определению ромба, параллелограмм с равными сторонами является ромбом.
Следовательно, MNKE — ромб.
Что и требовалось доказать.
б)
Дано: ABCD — прямоугольник.
AM = MB, BN = NC, CK = KD, AE = ED.
Доказать: MNKE — ромб.
Решение:
1. Рассмотрим треугольник ABD.
AM = MB (по условию), AE = ED (по условию).
ME является средней линией треугольника ABD, так как соединяет середины двух сторон (AM и AE).
Согласно теореме о средней линии, средняя линия треугольника параллельна основанию и равна половине основания:
ME = ½ BD.
2. Рассмотрим треугольник BCD.
BN = NC (по условию), CK = KD (по условию).
NK является средней линией треугольника BCD, так как соединяет середины двух сторон (BN и CK).
Согласно теореме о средней линии, средняя линия треугольника параллельна основанию и равна половине основания:
NK = ½ BD.
3. Рассмотрим треугольник ABC.
AM = MB (по условию), BN = NC (по условию).
MN является средней линией треугольника ABC, так как соединяет середины двух сторон (AM и BN).
Согласно теореме о средней линии, средняя линия треугольника параллельна основанию и равна половине основания:
MN = ½ AC.
4. Рассмотрим треугольник ADC.
AE = ED (по условию), CK = KD (по условию).
KE является средней линией треугольника ADC, так как соединяет середины двух сторон (AE и CK).
Согласно теореме о средней линии, средняя линия треугольника параллельна основанию и равна половине основания:
KE = ½ AC.
5. Поскольку MN параллельно AC, а KE параллельно AC, то MN параллельно KE.
6. Поскольку ME параллельно BD, а NK параллельно BD, то ME параллельно NK.
7. Поскольку ABCD — прямоугольник, его диагонали равны и делятся пополам. Следовательно, BD = AC, а также ME = NK = MN = KE.
8. MN параллельно KE, ME параллельно NK, а также ME = NK = MN = KE.
Таким образом, MNKE является параллелограммом, у которого все стороны равны.
Согласно определению ромба, параллелограмм с равными сторонами является ромбом.
Следовательно, MNKE — ромб.
Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!