ГДЗ по Геометрии 8 класс Номер 567 Атанасян — Подробные Ответы

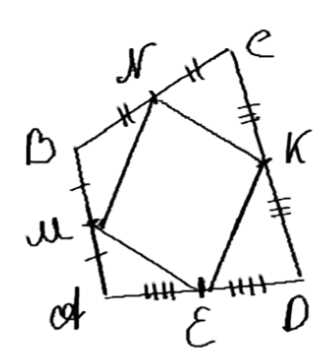
Докажите, что середины сторон произвольного четырёхугольника являются вершинами параллелограмма (теорема Вариньона).

Дано: ABCD — четырёхугольник; \(BN = NC\), \(CK = KD\), \(DE = ED\), \(BM = MA\).
Доказать: \(MNKE\) — параллелограмм.

Рассмотрим треугольник \(\triangle ABC\): \(BN = NC\) и \(BM = MA\), следовательно, \(NM\) — средняя линия (по определению). Значит:
\(
NM = \frac{1}{2}CA.
\)

Рассмотрим треугольник \(\triangle ADC\): \(CK = KD\) и \(AE = ED\), следовательно, \(KE\) — средняя линия (по определению). Значит:
\(
KE = \frac{1}{2}CA.
\)

Так как \(NM \parallel AC\) и \(KE \parallel AC\), то \(NM \parallel KE\).
Также \(KE = \frac{1}{2}CA\) и \(NM = \frac{1}{2}CA\), следовательно, \(KE = NM\).

Из \(NM \parallel KE\) и \(NM = KE\) следует, что \(MNKE\) — параллелограмм (по признаку параллелограмма).
Что и требовалось доказать.

Дано: ABCD — четырёхугольник; \(BN = NC\), \(CK = KD\), \(DE = ED\), \(BM = MA\).
Доказать: \(MNKE\) — параллелограмм.

Рассмотрим треугольник \(\triangle ABC\). По условию \(BN = NC\), то есть точка \(N\) — середина отрезка \(BC\). Также \(BM = MA\), то есть точка \(M\) — середина отрезка \(AB\). Соединяя точки \(M\) и \(N\), получаем, что \(MN\) — средняя линия треугольника \(\triangle ABC\). Из свойства средней линии треугольника следует, что она параллельна третьей стороне треугольника и равна половине её длины. Таким образом,
\(
MN \parallel AC \, \text{и} \, MN = \frac{1}{2}AC.
\)

Теперь рассмотрим треугольник \(\triangle ADC\). По условию \(CK = KD\), то есть точка \(K\) — середина отрезка \(CD\). Также \(AE = ED\), то есть точка \(E\) — середина отрезка \(AD\). Соединяя точки \(K\) и \(E\), получаем, что \(KE\) — средняя линия треугольника \(\triangle ADC\). Из свойства средней линии треугольника следует, что она параллельна третьей стороне треугольника и равна половине её длины. Таким образом,
\(
KE \parallel AC \, \text{и} \, KE = \frac{1}{2}AC.
\)

Так как \(MN \parallel AC\) и \(KE \parallel AC\), то \(MN \parallel KE\).
Также из равенств \(MN = \frac{1}{2}AC\) и \(KE = \frac{1}{2}AC\) следует, что \(MN = KE\).

Итак, \(MN \parallel KE\) и \(MN = KE\). Это означает, что противоположные стороны четырёхугольника \(MNKE\) равны и параллельны. Следовательно, по определению, \(MNKE\) является параллелограммом.

Что и требовалось доказать.