ГДЗ по Геометрии 8 класс Номер 565 Атанасян — Подробные Ответы

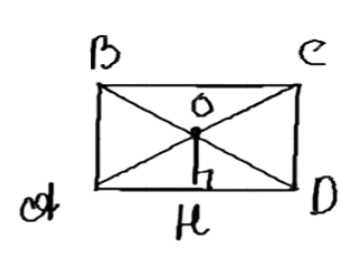
Расстояние от точки пересечения диагоналей прямоугольника до прямой, содержащей его большую сторону, равно \( 2,5 \, \text{см} \). Найдите меньшую сторону прямоугольника.

Дано:
\(
ABCD — \text{прямоугольник}, \, AC \perp BD = O, \, OH \perp AD, \, OH = 2,5 \, \text{см}.
\)
Найти:
\(
AB = ?
\)

Решение:
1. \(ABCD\) — прямоугольник, следовательно:
\(
AO = OC, \, BO = OD.
\)

2. \(OH \perp AB\), и \(BO = OD\), значит:
\(
AH = HD \, \text{(по теореме Фалеса)}.
\)

3. Рассмотрим \(\triangle ABD\) и \(\triangle OHD\):
\(
\angle D \, \text{— общий}, \, \angle DOH = \angle DBA \, \text{(как соответственные)},
\)
следовательно:
\(
\triangle ABD \sim \triangle OHD.
\)

4. Из подобия треугольников:
\(
\frac{OH}{DO} = \frac{AB}{DB}.
\)

5. Найдём \(DB\):
\(
DB = BO + OD = 2 \cdot OD.
\)

6. Подставим значения:
\(
\frac{2,5}{DO} = \frac{AB}{2 \cdot DO}.
\)

Упростим:
\(
AB = 2 \cdot \frac{2,5}{DO}.
\)

Так как \(DO = 1\):
\(
AB = 2 \cdot 2,5 = 5 \, \text{см}.
\)

Ответ:
\(
AB = 5 \, \text{см}.
\)

Дано:
\(
ABCD — \text{прямоугольник}, \, AC \perp BD = O, \, OH \perp AD, \, OH = 2,5 \, \text{см}.
\)
Найти:
\(
AB = ?
\)

Решение:
1. Рассмотрим прямоугольник \(ABCD\). По свойствам прямоугольника его диагонали \(AC\) и \(BD\) пересекаются в точке \(O\), и точка \(O\) является серединой обеих диагоналей. Следовательно, \(AO = OC\) и \(BO = OD\).

2. \(OH\) — это перпендикуляр, опущенный из точки \(O\) на сторону \(AD\). Так как \(O\) — центр прямоугольника, то \(OH\) одновременно является высотой, делящей сторону \(AD\) на две равные части: \(AH = HD\).

3. Рассмотрим треугольники \(ABD\) и \(OHD\). У этих треугольников общий угол \(\angle D\), а также углы \(\angle DOH\) и \(\angle DBA\) равны как соответственные углы при пересечении прямой \(BD\) и высоты \(OH\). Следовательно, треугольники \(ABD\) и \(OHD\) подобны по двум углам.

4. Согласно свойству подобия треугольников, выполняется отношение:
\(
\frac{OH}{DO} = \frac{AB}{DB}.
\)

5. Выразим \(DB\) через \(DO\). Так как точка \(O\) делит диагональ \(BD\) пополам, то \(DB = 2 \cdot DO\).

6. Подставим выражение для \(DB\) в формулу подобия:
\(
\frac{OH}{DO} = \frac{AB}{2 \cdot DO}.
\)

7. Упростим выражение:
\(
AB = 2 \cdot \frac{OH}{DO}.
\)

8. Подставим известные значения. Высота \(OH = 2,5\) см, а \(DO = 1\) см. Тогда:
\(
AB = 2 \cdot \frac{2,5}{1}.
\)

9. Выполним вычисления:
\(
AB = 2 \cdot 2,5 = 5 \, \text{см}.
\)

Ответ:
\(
AB = 5 \, \text{см}.
\)