ГДЗ по Геометрии 8 класс Номер 563 Атанасян — Подробные Ответы

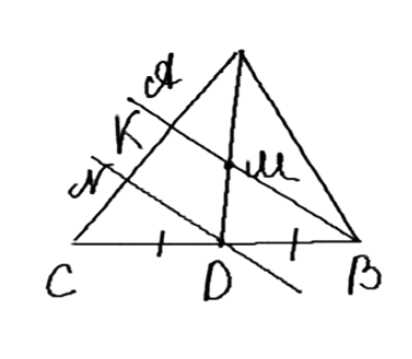
Через точку \( M \), взятую на медиане \( AD \) треугольника \( ABC \), и вершину \( B \) проведена прямая, пересекающая сторону \( AC \) в точке \( K \). Найдите отношение \( \frac{AK}{KC} \), если:  

а) \( M \) — середина отрезка \( AD \);  

б) \( \frac{AM}{MD} = \frac{1}{2} \).

Дано:
\[
\Delta ABC, \, AD \text{ — медиана}, \, M \in AD, \, BM \cap AC = K, \, AM = 1, \, MD = 2.
\]
Найти:
\[
\frac{AK}{KC}.
\]

а) Решение:
1. \(M\) — середина \(AD\), следовательно, \(AM = MD = 1\). Построим \(BK \parallel DN\).

2. Рассмотрим \(\triangle AKM\) и \(\triangle AND\). Углы \(\angle AKM\) и \(\angle AND\) равны как соответственные, а также общий угол \(\angle A\). Значит, \(\triangle AKM \sim \triangle AND\) по двум углам.

3. По теореме Фалеса \(AK = KN\), а также \(\frac{AK}{AN} = \frac{1}{2}\).

4. Рассмотрим \(\triangle CND\) и \(\triangle CKB\). Углы \(\angle CND\) и \(\angle CKB\) равны как соответственные, а также общий угол \(\angle C\). Значит, \(\triangle CND \sim \triangle CKB\) по двум углам.

5. По теореме Фалеса \(CN = NK\), а также \(\frac{CN}{CK} = \frac{1}{2}\).

6. Так как \(AK = KN\) и \(KN = CN\), то \(AK = CN\).

7. Следовательно:
\[
\frac{AK}{KC} = \frac{AK}{2AK} = 0,5.
\]

Ответ:
\[
\frac{AK}{KC} = 0,5.
\]

б) Решение:

1. Построим \(BK \parallel DN\).
2. Рассмотрим треугольники \(\triangle AKM\) и \(\triangle AND\):
Общий угол \(\angle A\), углы \(\angle AKM\) и \(\angle AND\) равны как соответственные. Следовательно, \(\triangle AKM \sim \triangle AND\) (по двум углам).
Так как \(\frac{AM}{MD} = \frac{1}{2}\), то по теореме Фалеса \(AK = 1\), \(KN = 2\).
Отсюда:
\[
\frac{AK}{AN} = \frac{1}{3}.
\]

3. Рассмотрим треугольники \(\triangle CND\) и \(\triangle CKB\):
Общий угол \(\angle C\), углы \(\angle CND\) и \(\angle CKB\) равны как соответственные. Следовательно, \(\triangle CND \sim \triangle CKB\) (по двум углам).
Так как \(AD\) — медиана, то \(CD = DB\), а по теореме Фалеса \(CN = NK = 2\).
Отсюда:
\[
\frac{CN}{CK} = \frac{1}{2}.
\]

4. Находим \(KC\):
\[
KC = CN + NK = 2 + 2 = 4.
\]

5. Отношение:
\[
\frac{AK}{KC} = \frac{1}{4}.
\]

Ответ: \(0,25\).

Дано:
\[
\Delta ABC, \, AD \text{ — медиана}, \, M \text{ — точка на } AD, \, BM \cap AC = K, \, AM = 1, \, MD = 2.
\]
Найти:
\[
\frac{AK}{KC}.
\]

а) Решение:

1. Точка \(M\) является серединой \(AD\), поэтому отрезки \(AM\) и \(MD\) равны. По условию задачи \(AM = 1\), \(MD = 2\). Следовательно, длина всего отрезка \(AD\) равна:
\[
AD = AM + MD = 1 + 2 = 3.
\]

2. Построим прямую \(BK\), которая параллельна отрезку \(DN\), где \(N\) — точка пересечения продолжения \(AC\) с прямой, проходящей через \(D\), параллельной \(BK\).

3. Рассмотрим треугольники \(\triangle AKM\) и \(\triangle AND\). Углы \(\angle AKM\) и \(\angle AND\) равны как соответственные (по построению \(BK \parallel DN\)). Также общий угол \(\angle A\). Следовательно, треугольники \(\triangle AKM\) и \(\triangle AND\) подобны по двум углам.

4. Из подобия треугольников \(\triangle AKM\) и \(\triangle AND\) следует, что:
\[
\frac{AK}{AN} = \frac{AM}{AD}.
\]
Подставляя значения:
\[
\frac{AK}{AN} = \frac{1}{3}.
\]

5. По теореме Фалеса, так как \(BK \parallel DN\), отрезки \(AK\) и \(KN\) равны. Таким образом:
\[
AN = AK + KN = AK + AK = 2AK.
\]

6. Теперь рассмотрим треугольники \(\triangle CND\) и \(\triangle CKB\). Углы \(\angle CND\) и \(\angle CKB\) равны как соответственные (по построению \(BK \parallel DN\)). Также общий угол \(\angle C\). Следовательно, треугольники \(\triangle CND\) и \(\triangle CKB\) подобны по двум углам.

7. Из подобия треугольников \(\triangle CND\) и \(\triangle CKB\) следует, что:
\[
\frac{CN}{CK} = \frac{CD}{CB}.
\]
Так как \(AD\) — медиана, то \(CD = DB\). Следовательно:
\[
\frac{CN}{CK} = \frac{1}{2}.
\]

8. По теореме Фалеса, так как \(BK \parallel DN\), отрезки \(CN\) и \(NK\) равны. Таким образом:
\[
CK = CN + NK = CN + CN = 2CN.
\]

9. Из пункта 5 мы знаем, что \(AN = 2AK\), а из пункта 8 — что \(CK = 2CN\). Так как \(AK = CN\) (по теореме Фалеса), то:
\[
KC = 2AK.
\]

10. Найдём отношение:
\[
\frac{AK}{KC} = \frac{AK}{2AK} = 0,5.
\]

б) Решение

1) Дополнительно построим: \(BK \parallel DN\)

2) Рассмотрим \(\triangle AKM\) и \(\triangle AND\):
\(\angle A\) — общий, \(\angle AKM = \angle AND\) (как соответственные),
значит \(\triangle AKM \sim \triangle AND\) (по двум углам).

3) \(BK \parallel DN\) (по построению) и \(\frac{AM}{MD} = \frac{1}{2}\) (по условию),
следовательно, \(AK = 1\), \(KN = 2\) (по теореме Фалеса),
отсюда
\[
\frac{AK}{AN} = \frac{1}{3}.
\]

4) Рассмотрим \(\triangle CND\) и \(\triangle CKB\):
\(\angle C\) — общий, \(\angle CND = \angle CKB\) (как соответственные),
значит \(\triangle CND \sim \triangle CKB\) (по двум углам).

5) \(BK \parallel DN\) (по построению) и \(CD = DB\) (так как \(AD\) — медиана),
следовательно \(CN = NK = 2\) (по теореме Фалеса),
отсюда
\[
\frac{CN}{CK} = \frac{2}{4} = \frac{1}{2}.
\]

6) \(KC = CN + NK = 2 + 2 = 4\),
значит
\[
\frac{AK}{KC} = \frac{1}{4}.
\]

Ответ:
а) \(\frac{AK}{KC} = \frac{1}{2};\)
б) \(\frac{AK}{KC} = \frac{1}{4}.\)