ГДЗ по Геометрии 8 класс Номер 552 Атанасян — Подробные Ответы

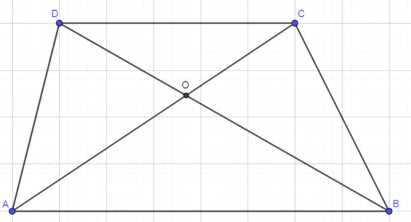
Диагонали трапеции \( ABCD \) с основаниями \( AB \) и \( CD \) пересекаются в точке \( O \). Найдите:  

а) \( AB \), если \( OB = 4 \, \text{см} \), \( OD = 10 \, \text{см} \), \( DC = 25 \, \text{см} \);  

б) \(\frac{AO}{OC}\) и \(\frac{BO}{OD}\), если \( AB = a \), \( DC = b \);  

в) \( AO \), если \( AB = 9,6 \, \text{дм} \), \( DC = 24 \, \text{см} \), \( AC = 15 \, \text{см} \).

Рассмотрим трапецию \(ABCD\), где \(DC \parallel AB\), а \(CA\) — секущая.

Углы \(\angle DCA\) и \(\angle CAB\) равны как накрестлежащие, а углы \(\angle DOC\) и \(\angle AOB\) равны как вертикальные. Следовательно, треугольники \(\triangle DOC\) и \(\triangle AOB\) подобны по двум углам. Из подобия следует пропорция:

\(
\frac{AB}{DC} = \frac{OB}{OC} = \frac{AO}{OD} = k.
\)

а) Найдем \(AB\):
\(
\frac{AB}{DC} = \frac{4}{10} \quad \Rightarrow \quad k = 0,4.
\)
\(
AB = 0,4 \cdot 25 = 10 \, \text{см}.
\)

б) Из подобия:
\(
\frac{AB}{DC} = \frac{a}{b} \quad \Rightarrow \quad k = \frac{a}{b}.
\)
\(
\frac{AO}{OC} = \frac{BO}{OD} = \frac{a}{b}.
\)

в) Найдем \(AO\):
\(
\frac{AO}{OC} = \frac{96}{24} = 4.
\)
\(
AO = 4 \quad \Rightarrow \quad AO = 4(15 — AO).
\)
\(
AC — AO = 60 — 4AO \quad \Rightarrow \quad 5AO = 60 \quad \Rightarrow \quad AO = 12 \, \text{см}.
\)

Ответ:
а) \(AB = 10 \, \text{см};\)
б) \(\frac{AO}{OC} = \frac{BO}{OD} = \frac{a}{b};\)
в) \(AO = 12 \, \text{см}.\)

Рассмотрим задачу. Нам дана трапеция \(ABCD\), где \(DC \parallel AB\), а диагонали \(AC\) и \(BD\) пересекаются в точке \(O\). Требуется найти величины, указанные в условиях, используя свойства подобия треугольников.

1. Рассмотрим секущую \(AC\), которая пересекает параллельные стороны \(DC\) и \(AB\). Углы \(\angle DCA\) и \(\angle CAB\) равны как накрестлежащие. Также углы \(\angle DOC\) и \(\angle AOB\) равны как вертикальные. Следовательно, треугольники \(\triangle DOC\) и \(\triangle AOB\) подобны по двум углам.

2. Из подобия треугольников \(\triangle DOC\) и \(\triangle AOB\) следует пропорциональность их сторон:
\(
\frac{AB}{DC} = \frac{OB}{OC} = \frac{AO}{OD} = k,
\)
где \(k\) — коэффициент подобия.

а) Найдем \(AB\). По условию, \(OB = 4 \, \text{см}\), \(OD = 10 \, \text{см}\), \(DC = 25 \, \text{см}\). Подставим данные в пропорцию:
\(
\frac{AB}{DC} = \frac{OB}{OD}.
\)
Подставляем значения:
\(
\frac{AB}{25} = \frac{4}{10}.
\)
Сократим дробь:
\(
\frac{AB}{25} = 0,4.
\)
Найдем \(AB\):
\(
AB = 25 \cdot 0,4 = 10 \, \text{см}.
\)

б) Найдем отношения \(\frac{AO}{OC}\) и \(\frac{BO}{OD}\). Пусть \(AB = a\), \(DC = b\). Тогда коэффициент подобия:
\(
k = \frac{a}{b}.
\)
Из подобия треугольников:
\(
\frac{AO}{OC} = \frac{BO}{OD} = k = \frac{a}{b}.
\)

в) Найдем \(AO\). По условию, \(AB = 9,6 \, \text{дм} = 96 \, \text{см}\), \(DC = 24 \, \text{см}\), \(AC = 15 \, \text{см}\). Найдем коэффициент подобия:
\(
\frac{AB}{DC} = \frac{96}{24} = 4.
\)
Следовательно:
\(
\frac{AO}{OC} = 4.
\)
Пусть \(AO = x\), тогда \(OC = AC — AO = 15 — x\). Подставим в пропорцию:
\(
\frac{AO}{OC} = 4 \quad \Rightarrow \quad \frac{x}{15 — x} = 4.
\)
Решим уравнение:
\(
x = 4(15 — x).
\)
Раскроем скобки:
\(
x = 60 — 4x.
\)
Перенесем \(4x\) в левую часть:
\(
5x = 60.
\)
Найдем \(x\):
\(
x = 12.
\)
Таким образом, \(AO = 12 \, \text{см}\).

Ответ:
а) \(AB = 10 \, \text{см};\)
б) \(\frac{AO}{OC} = \frac{BO}{OD} = \frac{a}{b};\)
в) \(AO = 12 \, \text{см}.\)