ГДЗ по Геометрии 8 класс Номер 543 Атанасян — Подробные Ответы

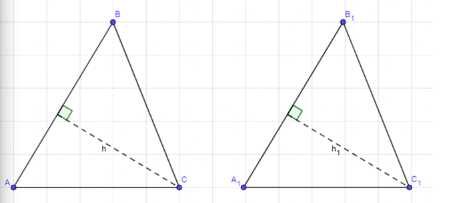
Докажите, что отношение сходственных сторон подобных треугольников равно отношению высот, проведённых к этим сторонам.

Дано: ΔABC ∼ ΔA₁B₁C₁, коэффициент подобия \(k\).
Необходимо доказать: \(\frac{AB}{A₁B₁} = \frac{h}{h₁}\).

Решение:
1. Согласно теореме об отношении площадей подобных треугольников:
\(
\frac{S_{ABC}}{S_{A₁B₁C₁}} = k^2
\)

2. Площадь треугольника равна:
\(
S = \frac{1}{2} \cdot основание \cdot высота
\)
Для треугольников ΔABC и ΔA₁B₁C₁:
\(
S_{ABC} = \frac{1}{2} \cdot AB \cdot h
\)
\(
S_{A₁B₁C₁} = \frac{1}{2} \cdot A₁B₁ \cdot h₁
\)

3. Подставляем площади в отношение:
\(
\frac{\frac{1}{2} \cdot AB \cdot h}{\frac{1}{2} \cdot A₁B₁ \cdot h₁} = k^2
\)

4. Упрощаем:
\(
\frac{AB \cdot h}{A₁B₁ \cdot h₁} = k^2
\)

5. Разделим обе стороны на \(k\):
\(
\frac{AB}{A₁B₁} \cdot \frac{h}{h₁} = k
\)

6. Следовательно:
\(
\frac{AB}{A₁B₁} = \frac{h}{h₁}
\)

Что и требовалось доказать.

Дано: ΔABC ∼ ΔA₁B₁C₁, коэффициент подобия \(k\).
Необходимо доказать: \(\frac{AB}{A₁B₁} = \frac{h}{h₁}\).

Решение:

1. Согласно теореме об отношении площадей подобных треугольников:
\(
\frac{S_{ABC}}{S_{A₁B₁C₁}} = k^2
\)

2. Площадь треугольника вычисляется по формуле:
\(
S = \frac{1}{2} \cdot основание \cdot высота
\)
Для треугольников ΔABC и ΔA₁B₁C₁ их площади выражаются следующим образом:
\(
S_{ABC} = \frac{1}{2} \cdot AB \cdot h
\)
\(
S_{A₁B₁C₁} = \frac{1}{2} \cdot A₁B₁ \cdot h₁
\)

3. Подставим выражения для площадей в отношение площадей:
\(
\frac{\frac{1}{2} \cdot AB \cdot h}{\frac{1}{2} \cdot A₁B₁ \cdot h₁} = k^2
\)

4. Сократим коэффициенты \( \frac{1}{2} \):
\(
\frac{AB \cdot h}{A₁B₁ \cdot h₁} = k^2
\)

5. Разделим обе стороны уравнения на \(k\):
\(
\frac{AB}{A₁B₁} \cdot \frac{h}{h₁} = k
\)

6. В силу равенства коэффициентов подобия сторон треугольников:
\(
\frac{AB}{A₁B₁} = k
\)
и высот:
\(
\frac{h}{h₁} = k
\)

7. Следовательно, из равенства коэффициентов подобия:
\(
\frac{AB}{A₁B₁} = \frac{h}{h₁}
\)

Что и требовалось доказать.