
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 540 Атанасян — Подробные Ответы
Периметр треугольника \( CDE \) равен \( 55 \, \text{см} \). В этот треугольник вписан ромб \( DMFN \) так, что вершины \( M, \, F \, \text{и} \, N \) лежат соответственно на сторонах \( CD, \, CE \, \text{и} \, DE \). Найдите стороны \( CD \) и \( DE \), если \( CF = 8 \, \text{см}, \, EF = 12 \, \text{см} \).
Дано: \( \triangle CDE \), \( DMFN \) — ромб, \( DF \) — диагональ ромба, \( DF \) — биссектриса, \( CF = 8 \, \text{см} \), \( EF = 12 \, \text{см} \), \( P_{CDE} = 55 \, \text{см} \). Найти: \( CD \) и \( DE \).
Решение:
1. По свойству ромба диагональ \( DF \) является биссектрисой. Следовательно, углы \( \angle MDF \) и \( \angle FDN \) равны.
2. Пропорция сторон:
\(
\frac{CD}{CF} = \frac{DE}{EF}
\)
Подставим значения:
\(
\frac{CD}{8} = \frac{DE}{12}
\)
3. Упростим пропорцию:
\(
\frac{CD}{8} = \frac{DE}{12} \Rightarrow CD = \frac{2}{3} DE
\)
4. Периметр треугольника \( \triangle CDE \):
\(
CD + DE + CE = P_{CDE}
\)
Подставим известные значения:
\(
CD + DE + CE = 55
\)
5. Найдем \( CE \):
\(
CE = CF + EF = 8 + 12 = 20 \, \text{см}
\)
6. Подставим \( CE \) в уравнение периметра:
\(
CD + DE = 55 — 20 = 35 \, \text{см}
\)
7. Используем \( CD = \frac{2}{3} DE \) и подставим в уравнение:
\(
\frac{2}{3} DE + DE = 35
\)
8. Сложим:
\(
\frac{2}{3} DE + \frac{3}{3} DE = \frac{5}{3} DE = 35
\)
9. Найдем \( DE \):
\(
DE = \frac{35}{\frac{5}{3}} = 35 \cdot \frac{3}{5} = 21 \, \text{см}
\)
10. Найдем \( CD \):
\(
CD = \frac{2}{3} DE = \frac{2}{3} \cdot 21 = 14 \, \text{см}
\)
Ответ: \( CD = 14 \, \text{см}, DE = 21 \, \text{см} \).
Дано: \( \triangle CDE \), \( DMFN \) — ромб, \( DF \) — диагональ ромба, \( DF \) — биссектриса, \( CF = 8 \, \text{см} \), \( EF = 12 \, \text{см} \), \( P_{CDE} = 55 \, \text{см} \). Найти: \( CD \) и \( DE \).
Решение:
1. По свойству ромба диагональ \( DF \) является биссектрисой углов \( \angle MDF \) и \( \angle FDN \). Это означает, что отношение сторон \( CD \) и \( DE \) пропорционально отношению сторон \( CF \) и \( FE \):
\(
\frac{CD}{CF} = \frac{DE}{FE}.
\)
2. Подставим известные значения \( CF = 8 \, \text{см} \) и \( FE = 12 \, \text{см} \):
\(
\frac{CD}{8} = \frac{DE}{12}.
\)
3. Упростим пропорцию, чтобы выразить \( CD \) через \( DE \):
\(
CD = \frac{8}{12} \cdot DE = \frac{2}{3} DE.
\)
4. Периметр треугольника \( \triangle CDE \) выражается как сумма всех его сторон:
\(
CD + DE + CE = P_{CDE}.
\)
Подставим известное значение периметра:
\(
CD + DE + CE = 55.
\)
5. Найдем \( CE \) как сумму \( CF \) и \( FE \), так как \( CE = CF + FE \):
\(
CE = 8 + 12 = 20 \, \text{см}.
\)
6. Подставим значение \( CE \) в уравнение периметра:
\(
CD + DE = 55 — 20 = 35 \, \text{см}.
\)
7. Используем ранее найденное выражение \( CD = \frac{2}{3} DE \) и подставим его в уравнение \( CD + DE = 35 \):
\(
\frac{2}{3} DE + DE = 35.
\)
8. Приведем к общему знаменателю:
\(
\frac{2}{3} DE + \frac{3}{3} DE = \frac{5}{3} DE.
\)
Таким образом, уравнение принимает вид:
\(
\frac{5}{3} DE = 35.
\)
9. Найдем \( DE \), умножив обе части уравнения на \( \frac{3}{5} \):
\(
DE = 35 \cdot \frac{3}{5} = \frac{105}{5} = 21 \, \text{см}.
\)
10. Теперь найдем \( CD \), используя выражение \( CD = \frac{2}{3} DE \):
\(
CD = \frac{2}{3} \cdot 21 = \frac{42}{3} = 14 \, \text{см}.
\)
11. Проверим решение. Сумма \( CD + DE + CE \) должна равняться периметру \( P_{CDE} \):
\(
CD + DE + CE = 14 + 21 + 20 = 55 \, \text{см}.
\)
Условие выполняется.
Ответ: \( CD = 14 \, \text{см}, DE = 21 \, \text{см}. \)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


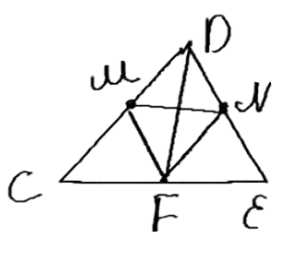

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!