
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 539 Атанасян — Подробные Ответы
В треугольник \( MNK \) вписан ромб \( MDEF \) так, что вершины \( D, \, E \, \text{и} \, F \) лежат соответственно на сторонах \( MN, \, NK \, \text{и} \, MK \). Найдите отрезки \( NE \) и \( EK \), если \( MN = 7 \, \text{см}, \, NK = 6 \, \text{см}, \, MK = 5 \, \text{см} \).
Дано: \( \triangle AMKN \), \( MFED \) — ромб, \( FE \in MK \), \( E \in KN \), \( D \in MN \), \( MN = 7 \, \text{см} \), \( NK = 6 \, \text{см} \), \( MK = 5 \, \text{см} \). Найти: \( NE \) и \( EK \).
Решение:
1. \( ME \) — диагональ ромба \( MFED \), следовательно, \( ME \) является биссектрисой. Значит, \( \angle FME = \angle EMD \), и по свойству биссектрисы:
\(
\frac{KE}{NE} = \frac{MK}{MN}.
\)
2. Подставим известные значения: \( MK = 5 \, \text{см} \), \( MN = 7 \, \text{см} \):
\(
\frac{KE}{NE} = \frac{5}{7}.
\)
3. Пусть \( NE = 6 — KE \) (так как \( NK = 6 \, \text{см} \)). Подставим это в пропорцию:
\(
\frac{KE}{6 — KE} = \frac{5}{7}.
\)
4. Преобразуем пропорцию:
\(
7 \cdot KE = 5 \cdot (6 — KE).
\)
5. Раскроем скобки:
\(
7 \cdot KE = 30 — 5 \cdot KE.
\)
6. Перенесем \( KE \) в одну часть уравнения:
\(
7 \cdot KE + 5 \cdot KE = 30.
\)
7. Сложим коэффициенты:
\(
12 \cdot KE = 30.
\)
8. Найдем \( KE \):
\(
KE = \frac{30}{12} = 2,5 \, \text{см}.
\)
9. Найдем \( NE \), используя \( NE = 6 — KE \):
\(
NE = 6 — 2,5 = 3,5 \, \text{см}.
\)
Ответ: \( NE = 3,5 \, \text{см}, EK = 2,5 \, \text{см} \).
Дано: \( \triangle AMKN \), \( MFED \) — ромб, \( FE \in MK \), \( E \in KN \), \( D \in MN \), \( MN = 7 \, \text{см} \), \( NK = 6 \, \text{см} \), \( MK = 5 \, \text{см} \). Найти: \( NE \) и \( EK \).
Решение:
1. Рассмотрим ромб \( MFED \). Его диагональ \( ME \) является биссектрисой углов \( \angle FMK \) и \( \angle EMN \) по свойству ромба. Следовательно, \( \angle FME = \angle EMD \).
2. Так как \( ME \) — биссектриса, то отрезки \( KE \) и \( NE \) на стороне \( KN \) делятся в отношении, равном отношению сторон \( MK \) и \( MN \):
\(
\frac{KE}{NE} = \frac{MK}{MN}.
\)
3. Подставим известные значения: \( MK = 5 \, \text{см} \), \( MN = 7 \, \text{см} \):
\(
\frac{KE}{NE} = \frac{5}{7}.
\)
4. Выразим \( NE \) через \( KE \). Поскольку \( NK = KE + NE = 6 \, \text{см} \), то:
\(
NE = 6 — KE.
\)
5. Подставим \( NE = 6 — KE \) в пропорцию:
\(
\frac{KE}{6 — KE} = \frac{5}{7}.
\)
6. Применим свойства пропорции и умножим крест-накрест:
\(
7 \cdot KE = 5 \cdot (6 — KE).
\)
7. Раскроем скобки в правой части:
\(
7 \cdot KE = 30 — 5 \cdot KE.
\)
8. Перенесем все слагаемые с \( KE \) в одну часть уравнения:
\(
7 \cdot KE + 5 \cdot KE = 30.
\)
9. Сложим коэффициенты:
\(
12 \cdot KE = 30.
\)
10. Найдем \( KE \), разделив обе части уравнения на 12:
\(
KE = \frac{30}{12} = 2 \frac{1}{2} \, \text{см}.
\)
11. Теперь найдем \( NE \), используя \( NE = 6 — KE \):
\(
NE = 6 — 2 \frac{1}{2} = 3 \frac{1}{2} \, \text{см}.
\)
Проверка: сумма \( KE + NE \) должна быть равна \( NK \):
\(
KE + NE = 2 \frac{1}{2} + 3 \frac{1}{2} = 6 \, \text{см}.
\)
Условие выполняется.
Ответ: \( NE = 3 \frac{1}{2} \, \text{см}, EK = 2 \frac{1}{2} \, \text{см} \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


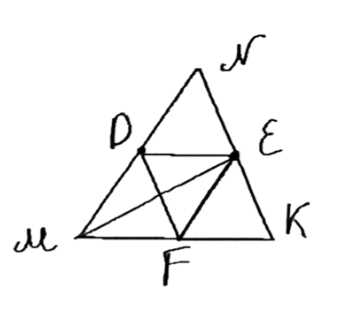

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!