Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
Ключевые особенности учебника:
1. Четкая структура:
Материал разбит на логически связанные разделы, каждый из которых посвящен отдельной теме, что облегчает восприятие и изучение.
2. Понятное изложение:
Доступный язык и стиль подачи материала делают даже сложные темы понятными для школьников.
3. Разнообразие задач:
Учебник содержит большое количество задач разной степени сложности, позволяя каждому ученику выбрать подходящие упражнения и совершенствовать свои навыки.
4. Наглядные иллюстрации:
Схемы и рисунки помогают лучше понять материал и визуализировать геометрические фигуры и их свойства.
5. Примеры из жизни:
Практические задачи, связанные с реальными ситуациями, делают изучение геометрии интересным и полезным.
6. Поддержка для учителей:
Методические рекомендации помогают преподавателям эффективно организовать уроки и использовать материал учебника.
Вывод:
Учебник Атанасяна по геометрии — это универсальный инструмент для изучения предмета, который сочетает понятность, практичность и разнообразие. Он подходит как для самостоятельного изучения, так и для работы в классе, делая процесс обучения более эффективным и увлекательным.
ГДЗ по Геометрии 8 класс Номер 531 Атанасян — Подробные Ответы
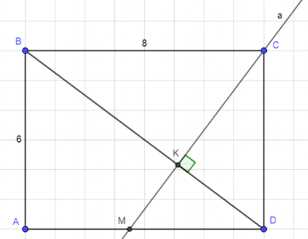
Стороны AB и BC прямоугольника ABCD равны соответственно 6 см и 8 см. Прямая, проходящая через вершину C и перпендикулярная к прямой BD, пересекает сторону AD в точке M, а диагональ BD — в точке K. Найдите площадь четырёхугольника ABKM.
Дано: \(ABCD\) — прямоугольник, \(AB = 6 \, \text{см}\), \(BC = 8 \, \text{см}\), \(BD\) — диагональ, \(CE \perp BD\), \(AD \cap CE = M\), \(BD \cap CE = K\). Найти площадь \(S_{ABKM}\).
Решение:
1. Вычислим диагональ \(BD\):
\(
BD^2 = AB^2 + AD^2 = 6^2 + 8^2 = 36 + 64 = 100, \quad BD = 10 \, \text{см}.
\)
2. Площадь треугольника \(S_{ABD} = S_{BCD}\) равна:
\(
S_{ABD} = \frac{1}{2} AB \cdot AD = \frac{1}{2} \cdot 6 \cdot 8 = 24 \, \text{см}^2.
\)
3. Площадь \(S_{BCD}\):
\(
S_{BCD} = \frac{1}{2} BD \cdot CK, \quad 24 = \frac{1}{2} \cdot 10 \cdot CK, \quad CK = 4,8 \, \text{см}.
\)
4. Рассмотрим \(\triangle CKD\) (прямоугольный):
\(
KD^2 = CD^2 — CK^2 = 6^2 — 4,8^2 = 36 — 23,04 = 12,96, \quad KD = 3,6 \, \text{см}.
\)
5. Площадь \(\triangle CDM\):
\(
S_{CDM} = \frac{1}{2} CD \cdot DM = \frac{1}{2} \cdot 6 \cdot DM = 3 \cdot DM.
\)
Также:
\(
S_{CDM} = \frac{1}{2} CM \cdot KD = \frac{1}{2} \cdot 3,6 \cdot CM = 1,8 \cdot CM.
\)
6. Выразим \(CM\):
\(
3 \cdot DM = 1,8 \cdot CM, \quad CM = \sqrt{CD^2 + MD^2} = \sqrt{36 + MD^2}.
\)
Подставим:
\(
1,8 \sqrt{36 + MD^2} = 3 \cdot MD.
\)
7. Решим уравнение:
\(
MD = 0,6 \sqrt{36 + MD^2}, \quad MD^2 = 0,36 (36 + MD^2), \)
\(\quad MD^2 = 12,96 + 0,36 MD^2, \quad 0,64 MD^2 = 12,96.
\)
\(
MD^2 = \frac{12,96}{0,64} = 20,25, \quad MD = \sqrt{20,25} = 4,5 \, \text{см}.
\)
8. Найдём \(KM\):
\(
KM^2 = MD^2 — KD^2 = 20,25 — 12,96 = 7,29, \quad KM = \sqrt{7,29} = 2,7 \, \text{см}.
\)
9. Площадь \(\triangle DKM\):
\(
S_{DKM} = \frac{1}{2} KD \cdot KM = \frac{1}{2} \cdot 3,6 \cdot 2,7 = 4,86 \, \text{см}^2.
\)
10. Площадь \(S_{ABKM}\):
\(
S_{ABKM} = S_{ABD} — S_{DKM} = 24 — 4,86 = 19,14 \, \text{см}^2.
\)
Ответ: \(19,14 \, \text{см}^2\).
Дано: \(ABCD\) — прямоугольник, \(AB = 6 \, \text{см}\), \(BC = 8 \, \text{см}\), \(BD\) — диагональ, \(CE \perp BD\), \(AD \cap CE = M\), \(BD \cap CE = K\). Найти площадь \(S_{ABKM}\).
Решение:
1. Вычислим длину диагонали \(BD\) прямоугольника по теореме Пифагора:
\(
BD^2 = AB^2 + AD^2 = 6^2 + 8^2 = 36 + 64 = 100.
\)
\(
BD = \sqrt{100} = 10 \, \text{см}.
\)
2. Площадь треугольника \(S_{ABD}\) равна:
\(
S_{ABD} = \frac{1}{2} AB \cdot AD = \frac{1}{2} \cdot 6 \cdot 8 = 24 \, \text{см}^2.
\)
Так как диагональ \(BD\) делит прямоугольник на два равных треугольника, то:
\(
S_{ABD} = S_{BCD} = 24 \, \text{см}^2.
\)
3. Площадь треугольника \(S_{BCD}\) также можно выразить через длину диагонали \(BD\) и высоту \(CK\):
\(
S_{BCD} = \frac{1}{2} BD \cdot CK.
\)
Подставим известные значения:
\(
24 = \frac{1}{2} \cdot 10 \cdot CK.
\)
Решим уравнение:
\(
CK = \frac{24 \cdot 2}{10} = 4,8 \, \text{см}.
\)
4. Рассмотрим прямоугольный треугольник \(\triangle CKD\). Найдём длину \(KD\) по теореме Пифагора:
\(
KD^2 = CD^2 — CK^2 = 6^2 — 4,8^2 = 36 — 23,04 = 12,96.
\)
\(
KD = \sqrt{12,96} = 3,6 \, \text{см}.
\)
5. Найдём площадь треугольника \(\triangle CDM\) двумя способами. Первый способ:
\(
S_{CDM} = \frac{1}{2} CD \cdot DM = \frac{1}{2} \cdot 6 \cdot DM = 3 \cdot DM.
\)
Второй способ:
\(
S_{CDM} = \frac{1}{2} CM \cdot KD = \frac{1}{2} \cdot 3,6 \cdot CM = 1,8 \cdot CM.
\)
Приравняем площади:
\(
3 \cdot DM = 1,8 \cdot CM.
\)
6. Выразим \(CM\) через \(CD\) и \(MD\) по теореме Пифагора:
\(
CM = \sqrt{CD^2 + MD^2} = \sqrt{6^2 + MD^2} = \sqrt{36 + MD^2}.
\)
Подставим в уравнение:
\(
1,8 \sqrt{36 + MD^2} = 3 \cdot MD.
\)
Решим уравнение:
\(
MD = 0,6 \sqrt{36 + MD^2}.
\)
Возведём обе части в квадрат:
\(
MD^2 = 0,36 (36 + MD^2).
\)
Раскроем скобки:
\(
MD^2 = 12,96 + 0,36 MD^2.
\)
Перенесём \(0,36 MD^2\) в левую часть:
\(
MD^2 — 0,36 MD^2 = 12,96.
\)
\(
0,64 MD^2 = 12,96.
\)
\(
MD^2 = \frac{12,96}{0,64} = 20,25.
\)
\(
MD = \sqrt{20,25} = 4,5 \, \text{см}.
\)
7. Найдём длину \(KM\) по теореме Пифагора:
\(
KM^2 = MD^2 — KD^2 = 20,25 — 12,96 = 7,29.
\)
\(
KM = \sqrt{7,29} = 2,7 \, \text{см}.
\)
8. Найдём площадь треугольника \(\triangle DKM\):
\(
S_{DKM} = \frac{1}{2} KD \cdot KM = \frac{1}{2} \cdot 3,6 \cdot 2,7.
\)
Выполним вычисления:
\(
S_{DKM} = \frac{1}{2} \cdot 9,72 = 4,86 \, \text{см}^2.
\)
9. Найдём площадь \(S_{ABKM}\):
\(
S_{ABKM} = S_{ABD} — S_{DKM}.
\)
Подставим значения:
\(
S_{ABKM} = 24 — 4,86 = 19,14 \, \text{см}^2.
\)
Ответ: \(19 \, \frac{7}{50} \, \text{см}^2\) или \(19,14 \, \text{см}^2\).
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.