
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 530 Атанасян — Подробные Ответы
В равнобедренном треугольнике ABC с основанием BC высота AD равна 8 см. Найдите площадь треугольника ABC, если медиана DM треугольника ADC равна 8 см.
Дано: треугольник \( \triangle ABC \) равнобедренный (\( AB = AC \)), высота \( AD \perp BC \), \( AD = 8 \, \text{см} \), \( DM = 8 \, \text{см} \), \( AM = MC \). Найти площадь треугольника \( S_{\triangle ABC} \).
Решение:
1. Построим прямые \( AE \parallel BC \) и \( EC \parallel AD \). Так как \( BC \perp AD \), то \( AE \perp EC \), следовательно, \( AEDC \) — прямоугольник.
По свойству прямоугольника: \( DM = ME = AM = MC = 8 \, \text{см} \).
2. Найдём \( AC \):
\(
AC = AM + MC = 2DM = 16 \, \text{см}.
\)
3. Вычислим \( DC \) по теореме Пифагора:
\(
DC^2 = AC^2 — AD^2 = 16^2 — 8^2 = 256 — 64 = 192.
\)
\(
DC = \sqrt{192} = \sqrt{64 \cdot 3} = 8\sqrt{3} \, \text{см}.
\)
4. Треугольник \( \triangle ABC \) равнобедренный, \( AD \) — высота, значит \( AD \) является медианой, следовательно:
\(
BD = DC = 8\sqrt{3} \, \text{см}.
\)
5. Найдём \( BC \):
\(
BC = BD + DC = 8\sqrt{3} + 8\sqrt{3} = 16\sqrt{3} \, \text{см}.
\)
6. Найдём площадь треугольника \( \triangle ABC \):
\(
S_{\triangle ABC} = \frac{1}{2} BC \cdot AD = \frac{1}{2} \cdot 16\sqrt{3} \cdot 8 = 64\sqrt{3} \, \text{см}^2.
\)
Ответ: площадь треугольника \( S_{\triangle ABC} = 64\sqrt{3} \, \text{см}^2 \).
Дано: треугольник \( \triangle ABC \) равнобедренный (\( AB = AC \)), высота \( AD \perp BC \), \( AD = 8 \, \text{см} \), \( DM = 8 \, \text{см} \), \( AM = MC \). Найти площадь треугольника \( S_{\triangle ABC} \).
Решение:
1. Построим прямые \( AE \parallel BC \) и \( EC \parallel AD \). Так как \( BC \perp AD \), то \( AE \perp EC \). Следовательно, четырёхугольник \( AEDC \) является прямоугольником.
По свойству прямоугольника, противоположные стороны равны: \( DM = ME = AM = MC = 8 \, \text{см} \).
2. Найдём длину стороны \( AC \). Так как \( AM = MC = 8 \, \text{см} \), то:
\(
AC = AM + MC = 8 + 8 = 16 \, \text{см}.
\)
3. Рассчитаем длину \( DC \) по теореме Пифагора. В прямоугольном треугольнике \( \triangle ADC \):
\(
DC^2 = AC^2 — AD^2.
\)
Подставим значения:
\(
DC^2 = 16^2 — 8^2 = 256 — 64 = 192.
\)
Вычислим корень:
\(
DC = \sqrt{192} = \sqrt{64 \cdot 3} = \sqrt{64} \cdot \sqrt{3} = 8\sqrt{3} \, \text{см}.
\)
4. Так как треугольник \( \triangle ABC \) равнобедренный, а \( AD \) является высотой, то \( AD \) также является медианой. Следовательно, медиана делит основание \( BC \) пополам, и:
\(
BD = DC = 8\sqrt{3} \, \text{см}.
\)
5. Найдём длину основания \( BC \):
\(
BC = BD + DC = 8\sqrt{3} + 8\sqrt{3} = 16\sqrt{3} \, \text{см}.
\)
6. Теперь найдём площадь треугольника \( \triangle ABC \). Формула площади треугольника:
\(
S_{\triangle ABC} = \frac{1}{2} BC \cdot AD.
\)
Подставим значения:
\(
S_{\triangle ABC} = \frac{1}{2} \cdot 16\sqrt{3} \cdot 8.
\)
Выполним умножение:
\(
S_{\triangle ABC} = \frac{1}{2} \cdot 128\sqrt{3} = 64\sqrt{3} \, \text{см}^2.
\)
Ответ: площадь треугольника \( S_{\triangle ABC} = 64\sqrt{3} \, \text{см}^2 \).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


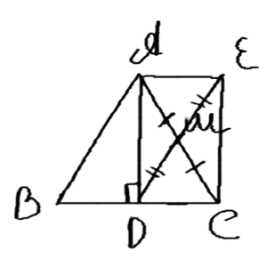

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!