ГДЗ по Геометрии 8 класс Номер 527 Атанасян — Подробные Ответы

В равнобедренной трапеции диагональ равна 10 см, а высота равна 6 см. Найдите площадь трапеции.

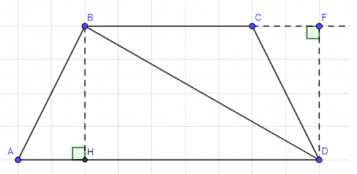
Дано: \(ABCD\) — равнобедренная трапеция, \(BH = 6\) см, \(BD = 10\) см.

Требуется найти площадь трапеции \(S_{ABCD}\).

1. Построим перпендикуляр \(DF \perp BC\), где \(F\) — точка пересечения. Рассмотрим треугольники \(\triangle ABH\) и \(\triangle CFD\). Они равны по гипотенузе и катету (\(AB = CD\), \(BH = FD\)), следовательно, \(CF = AH\).

2. Найдем \(HD\) через теорему Пифагора в треугольнике \(\triangle BHD\):
\(
BD^2 = BH^2 + HD^2,
\)
\(
10^2 = 6^2 + HD^2,
\)
\(
HD^2 = 100 — 36 = 64,
\)
\(
HD = \sqrt{64} = 8 \, \text{см}.
\)

3. Найдем площадь одного треугольника \(S_{BHD}\):
\(
S_{BHD} = \frac{1}{2} \cdot BH \cdot HD = \frac{1}{2} \cdot 6 \cdot 8 = 24 \, \text{см}^2.
\)

4. Площадь трапеции составит:
\(
S_{ABCD} = 2 \cdot S_{BHD} = 2 \cdot 24 = 48 \, \text{см}^2.
\)

Ответ: \(S_{ABCD} = 48\) см\(^2\).

Дано: \(ABCD\) — равнобедренная трапеция, \(BH = 6\) см, \(BD = 10\) см.
Требуется найти площадь трапеции \(S_{ABCD}\).

Шаг 1. Построим перпендикуляр \(DF \perp BC\), где \(F\) — точка пересечения.
Поскольку трапеция равнобедренная (\(AB = CD\)), высоты \(BH\) и \(DF\) равны (\(BH = DF = 6\) см). Отрезки \(AH\) и \(CF\) также равны, так как равнобедренная трапеция симметрична относительно средней линии.

Шаг 2. Рассмотрим треугольник \(\triangle BHD\). В этом треугольнике гипотенуза \(BD = 10\) см, один из катетов \(BH = 6\) см. Найдем второй катет \(HD\) с использованием теоремы Пифагора:
\(
BD^2 = BH^2 + HD^2.
\)
Подставим известные значения:
\(
10^2 = 6^2 + HD^2,
\)
\(
100 = 36 + HD^2,
\)
\(
HD^2 = 100 — 36 = 64,
\)
\(
HD = \sqrt{64} = 8 \, \text{см}.
\)

Шаг 3. Найдем площадь треугольника \(\triangle BHD\). Формула площади треугольника:
\(
S_{\triangle} = \frac{1}{2} \cdot a \cdot h,
\)
где \(a\) — основание, \(h\) — высота. В нашем случае основание \(HD = 8\) см, высота \(BH = 6\) см. Подставим значения:
\(
S_{BHD} = \frac{1}{2} \cdot 8 \cdot 6 = \frac{48}{2} = 24 \, \text{см}^2.
\)

Шаг 4. Поскольку трапеция симметрична, площадь трапеции \(S_{ABCD}\) состоит из двух равных треугольников \(\triangle BHD\) и \(\triangle CFD\). Следовательно:
\(
S_{ABCD} = 2 \cdot S_{BHD}.
\)
Подставим значение площади одного треугольника:
\(
S_{ABCD} = 2 \cdot 24 = 48 \, \text{см}^2.
\)

Ответ: площадь трапеции \(S_{ABCD} = 48\) см\(^2\).