
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 526 Атанасян — Подробные Ответы
В ромбе высота, равная \(\frac{4\sqrt{2}}{6}\) см, составляет большей диагонали. Найдите площадь ромба.
Дано:
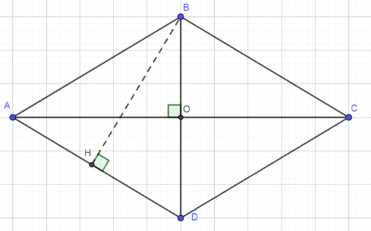
— Высота ромба \(BH = \frac{4\sqrt{2}}{6}\) см, которая составляет часть большей диагонали \(BD\).
— Требуется найти площадь ромба \(S_{ABCD}\).
1. Найдем сторону ромба \(AC\):
Высота \(BH\) делит сторону ромба \(AC\) на две равные части, следовательно:
\(
\frac{2}{3}AC = \frac{4\sqrt{2}}{6}.
\)
Умножим обе стороны на \(\frac{3}{2}\):
\(
AC = \frac{4\sqrt{2}}{6} \cdot \frac{3}{2} = \sqrt{2}.
\)
2. Формула площади ромба:
Площадь ромба равна половине произведения его диагоналей:
\(
S_{ABCD} = \frac{1}{2}BD \cdot AC.
\)
Также площадь ромба можно выразить через высоту и сторону:
\(
S_{ABCD} = BH \cdot AD.
\)
3. Найдем большую диагональ \(BD\):
Из условия известно, что высота \(BH\) составляет \(\frac{2}{3}\) большей диагонали \(BD\):
\(
\frac{1}{2}BD = \frac{2}{3}AD \Rightarrow BD = \frac{4}{3}AD.
\)
4. Рассмотрим прямоугольный треугольник \(\triangle AOD:\)
Диагонали ромба пересекаются под прямым углом, поэтому:
\(
AD^2 = AO^2 + OD^2.
\)
Подставим значения:
\(
AO = \frac{AC}{2} = \frac{\sqrt{2}}{2}, \quad OD = \frac{2}{3}AD.
\)
Следовательно:
\(
AD^2 = \left(\frac{\sqrt{2}}{2}\right)^2 + \left(\frac{2}{3}AD\right)^2.
\)
Рассчитаем:
\(
AD^2 = \frac{1}{2} + \frac{4}{9}AD^2.
\)
Приведем к общему знаменателю:
\(
AD^2 — \frac{4}{9}AD^2 = \frac{1}{2}.
\)
\(
\frac{5}{9}AD^2 = \frac{1}{2}.
\)
Найдем \(AD^2\):
\(
AD^2 = \frac{9}{10} \Rightarrow AD = \frac{3}{\sqrt{10}}.
\)
5. Вычислим площадь ромба:
Используем формулу площади через высоту и сторону:
\(
S_{ABCD} = BH \cdot AD.
\)
Подставим значения:
\(
S_{ABCD} = \frac{4\sqrt{2}}{6} \cdot \frac{3}{\sqrt{10}} = \frac{2\sqrt{2}}{\sqrt{10}}.
\)
Упростим выражение:
\(
S_{ABCD} = \frac{2\sqrt{2} \cdot \sqrt{10}}{10} = \frac{2\sqrt{5}}{5} \, \text{см}^2.
\)
Ответ:
Площадь ромба равна \(\frac{2\sqrt{5}}{5}\) см\(^2\).
Дано:
Высота ромба \(BH = \frac{4\sqrt{2}}{6}\) см, которая составляет часть большей диагонали \(BD\).
Требуется найти площадь ромба \(S_{ABCD}\).
1. Найдем сторону ромба \(AC\).
Высота \(BH\) делит сторону ромба \(AC\) на две равные части, следовательно:
\(
\frac{2}{3}AC = \frac{4\sqrt{2}}{6}.
\)
Умножим обе стороны на \(\frac{3}{2}\):
\(
AC = \frac{4\sqrt{2}}{6} \cdot \frac{3}{2} = \sqrt{2}.
\)
Таким образом, сторона ромба \(AC = \sqrt{2}\) см.
2. Формула площади ромба.
Площадь ромба равна половине произведения его диагоналей:
\(
S_{ABCD} = \frac{1}{2}BD \cdot AC.
\)
Также площадь ромба можно выразить через высоту и сторону:
\(
S_{ABCD} = BH \cdot AD.
\)
3. Найдем большую диагональ \(BD\).
Из условия известно, что высота \(BH\) составляет \(\frac{2}{3}\) большей диагонали \(BD\):
\(
\frac{1}{2}BD = \frac{2}{3}AD \Rightarrow BD = \frac{4}{3}AD.
\)
4. Рассмотрим прямоугольный треугольник \(AOD\).
Диагонали ромба пересекаются под прямым углом, поэтому:
\(
AD^2 = AO^2 + OD^2.
\)
Подставим значения:
\(
AO = \frac{AC}{2} = \frac{\sqrt{2}}{2}, \quad OD = \frac{2}{3}AD.
\)
Следовательно:
\(
AD^2 = \left(\frac{\sqrt{2}}{2}\right)^2 + \left(\frac{2}{3}AD\right)^2.
\)
Рассчитаем:
\(
AD^2 = \frac{1}{2} + \frac{4}{9}AD^2.
\)
Приведем к общему знаменателю:
\(
AD^2 — \frac{4}{9}AD^2 = \frac{1}{2}.
\)
\(
\frac{5}{9}AD^2 = \frac{1}{2}.
\)
Найдем \(AD^2\):
\(
AD^2 = \frac{9}{10}.
\)
Возьмем корень:
\(
AD = \sqrt{\frac{9}{10}} = \frac{3}{\sqrt{10}} = \frac{3\sqrt{10}}{10}.
\)
5. Найдем площадь ромба.
Используем формулу площади через высоту и сторону:
\(
S_{ABCD} = BH \cdot AD.
\)
Подставим значения:
\(
S_{ABCD} = \frac{4\sqrt{2}}{6} \cdot \frac{3\sqrt{10}}{10}.
\)
Упростим выражение:
\(
S_{ABCD} = \frac{4 \cdot 3 \cdot \sqrt{2} \cdot \sqrt{10}}{6 \cdot 10} = \frac{12\sqrt{20}}{60}.
\)
Сократим дробь:
\(
S_{ABCD} = \frac{\sqrt{20}}{5}.
\)
Представим корень в упрощенном виде:
\(
\sqrt{20} = \sqrt{4 \cdot 5} = 2\sqrt{5}.
\)
Следовательно:
\(
S_{ABCD} = \frac{2\sqrt{5}}{5}.
\)
Ответ:
Площадь ромба равна \(
S_{ABCD} = \frac{2\sqrt{5}}{5}.
\) или \(0,894\) см\(^2\) (округлено до тысячных).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!