Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
Ключевые особенности учебника:
1. Четкая структура:
Материал разбит на логически связанные разделы, каждый из которых посвящен отдельной теме, что облегчает восприятие и изучение.
2. Понятное изложение:
Доступный язык и стиль подачи материала делают даже сложные темы понятными для школьников.
3. Разнообразие задач:
Учебник содержит большое количество задач разной степени сложности, позволяя каждому ученику выбрать подходящие упражнения и совершенствовать свои навыки.
4. Наглядные иллюстрации:
Схемы и рисунки помогают лучше понять материал и визуализировать геометрические фигуры и их свойства.
5. Примеры из жизни:
Практические задачи, связанные с реальными ситуациями, делают изучение геометрии интересным и полезным.
6. Поддержка для учителей:
Методические рекомендации помогают преподавателям эффективно организовать уроки и использовать материал учебника.
Вывод:
Учебник Атанасяна по геометрии — это универсальный инструмент для изучения предмета, который сочетает понятность, практичность и разнообразие. Он подходит как для самостоятельного изучения, так и для работы в классе, делая процесс обучения более эффективным и увлекательным.
ГДЗ по Геометрии 8 класс Номер 523 Атанасян — Подробные Ответы
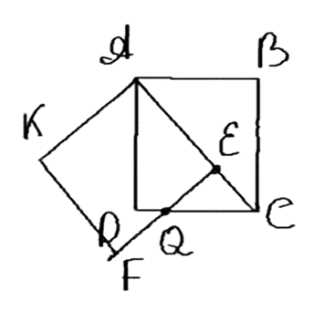
Два квадрата со стороной \[a\] имеют одну общую вершину, причём сторона одного из них лежит на диагонали другого. Найдите площадь общей части этих квадратов.
Дано: \(ABCD\) и \(AEFK\) — квадраты; \(AB = AF = a\).
Найти: \(S_{AEOD}\).
Решение:
1) \(S_{AEOD} = S_{ACD} — S_{ECQ}\).
2) \(S_{ACD} = \frac{1}{2} \cdot AD \cdot DC = \frac{1}{2} \cdot a \cdot a = \frac{a^2}{2}\).
3) \(AC^2 = AD^2 + DC^2 = a^2 + a^2 = 2a^2\); \(AC = a\sqrt{2}\).
4) \(EC = AC — AE = a\sqrt{2} — a = a(\sqrt{2} — 1)\).
5) Треугольник \(ECQ\) — прямоугольный и равнобедренный, так как \(\angle ECQ = 45^\circ\).
Следовательно, \(EQ = EC\).
6) \(S_{ECQ} = \frac{1}{2} \cdot QE \cdot EC = \frac{1}{2} \cdot EC^2 = \frac{1}{2} \cdot a^2(\sqrt{2} — 1)^2 = \frac{1}{2} \cdot a^2(3 — 2\sqrt{2})\).
7) \(S_{AEOD} = \frac{a^2}{2} — \frac{1}{2} \cdot a^2(3 — 2\sqrt{2}) = \frac{a^2}{2}(1 — 3 + 2\sqrt{2}) = \frac{a^2}{2}(2\sqrt{2} — 2) = a^2(\sqrt{2} — 1)\).
Ответ: \(a^2(\sqrt{2} — 1)\).
Дано: \(ABCD\) и \(AEFK\) — квадраты; \(AB = AF = a\).
Найти: \(S_{AEOD}\).
Решение:
1) Площадь фигуры \(AEOD\) можно найти как разность площадей треугольника \(ACD\) и треугольника \(ECQ\):
\[S_{AEOD} = S_{ACD} — S_{ECQ}.\]
2) Найдем площадь треугольника \(ACD\). Так как \(ABCD\) — квадрат, то \(AD = DC = a\). Площадь прямоугольного треугольника \(ACD\) вычисляется по формуле:
\[S_{ACD} = \frac{1}{2} \cdot AD \cdot DC = \frac{1}{2} \cdot a \cdot a = \frac{a^2}{2}.\]
3) Найдем длину диагонали \(AC\) квадрата \(ABCD\). По теореме Пифагора:
\[AC^2 = AD^2 + DC^2 = a^2 + a^2 = 2a^2,\]
\[AC = a\sqrt{2}.\]
4) Найдем длину отрезка \(EC\). Так как \(AEFK\) — квадрат, то \(AE = a\). Тогда:
\[EC = AC — AE = a\sqrt{2} — a = a(\sqrt{2} — 1).\]
5) Рассмотрим треугольник \(ECQ\). Так как \(AC\) — диагональ квадрата, то угол между \(AC\) и \(EF\) равен \(45^\circ\). Следовательно, треугольник \(ECQ\) — прямоугольный и равнобедренный, так как \(\angle ECQ = 45^\circ\). Поэтому:
\[EQ = EC = a(\sqrt{2} — 1).\]
6) Найдем площадь треугольника \(ECQ\). Площадь прямоугольного треугольника вычисляется по формуле:
\[S_{ECQ} = \frac{1}{2} \cdot QE \cdot EC = \frac{1}{2} \cdot EC^2 = \frac{1}{2} \cdot a^2(\sqrt{2} — 1)^2.\]
Раскроем квадрат:
\[(\sqrt{2} — 1)^2 = 2 — 2\sqrt{2} + 1 = 3 — 2\sqrt{2}.\]
Подставим:
\[S_{ECQ} = \frac{1}{2} \cdot a^2(3 — 2\sqrt{2}) = \frac{a^2}{2}(3 — 2\sqrt{2}).\]
7) Найдем площадь фигуры \(AEOD\):
\[S_{AEOD} = S_{ACD} — S_{ECQ} = \frac{a^2}{2} — \frac{a^2}{2}(3 — 2\sqrt{2}).\]
Вынесем \(\frac{a^2}{2}\) за скобки:
\[S_{AEOD} = \frac{a^2}{2}(1 — 3 + 2\sqrt{2}) = \frac{a^2}{2}(2\sqrt{2} — 2).\]
Упростим:
\[S_{AEOD} = \frac{a^2}{2} \cdot 2(\sqrt{2} — 1) = a^2(\sqrt{2} — 1).\]
Ответ: \(a^2(\sqrt{2} — 1)\).
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.