
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 522 Атанасян — Подробные Ответы
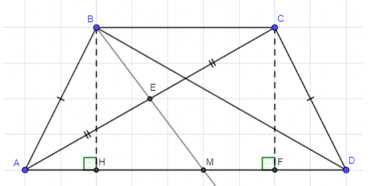
В равнобедренной трапеции ABCD с основаниями \(AD = 17\) см, \(BC = 5\) см и боковой стороной \(AB = 10\) см через вершину B проведена прямая, делящая диагональ AC пополам и пересекающая основание AD в точке M. Найдите площадь треугольника BDM.
Дано: \(ABCD\) — равнобедренная трапеция; \(AD = 17\) см; \(BC = 5\) см; \(AB = 10\) см; \(BE \perp AC = E\); \(AE = EC\); \(BE \perp AD = M\).
Найти: \(S_{BDM}\).
Решение:
1) \(AH = FD = \frac{AD — BC}{2} = \frac{17 — 5}{2} = 6\) см.
2) В прямоугольном треугольнике \(AHB\):
\(BH^2 = AB^2 — AH^2 = 100 — 36 = 64\);
\(BH = 8\) см.
3) Треугольники \(AEM\) и \(BEC\) равны по стороне и двум прилежащим углам, так как \(AE = EC\), \(\angle BEC = \angle AEM\) (вертикальные), \(\angle CAD = \angle BCA\) (накрестлежащие).
Следовательно, \(AM = BC = 5\) см.
4) \(MD = AD — AM = 17 — 5 = 12\) см.
5) Площадь треугольника \(BDM\):
\(S_{BDM} = \frac{1}{2} \cdot MD \cdot BH = \frac{1}{2} \cdot 12 \cdot 8 = 48\) см².
Ответ: \(48\) см².
Дано: \(ABCD\) — равнобедренная трапеция; \(AD = 17\) см; \(BC = 5\) см; \(AB = 10\) см; \(BE \perp AC = E\); \(AE = EC\); \(BE \perp AD = M\).
Найти: \(S_{BDM}\).
Решение:
1) Поскольку \(ABCD\) — равнобедренная трапеция, её боковые стороны равны: \(AB = CD = 10\) см.
2) Найдем высоту трапеции. Для этого проведем перпендикуляры \(AH\) и \(FD\) из вершин \(A\) и \(D\) на основание \(BC\).
Так как трапеция равнобедренная, отрезки \(AH\) и \(FD\) равны.
Длина основания \(AD = 17\) см, длина основания \(BC = 5\) см.
Разность оснований: \(AD — BC = 17 — 5 = 12\) см.
Так как \(AH = FD\), то каждый из них равен половине разности оснований:
\(AH = FD = \frac{12}{2} = 6\) см.
3) Рассмотрим прямоугольный треугольник \(AHB\). В нем известны катет \(AH = 6\) см и гипотенуза \(AB = 10\) см.
По теореме Пифагора найдем второй катет \(BH\):
\(BH^2 = AB^2 — AH^2 = 100 — 36 = 64\);
\(BH = \sqrt{64} = 8\) см.
Таким образом, высота трапеции \(BH = 8\) см.
4) Рассмотрим диагональ \(AC\) и точку \(E\), которая является серединой диагонали, так как \(AE = EC\).
Проведем перпендикуляр \(BE\) к диагонали \(AC\).
Так как \(BE \perp AC\), то треугольники \(AEM\) и \(BEC\) прямоугольные.
5) Рассмотрим треугольники \(AEM\) и \(BEC\):
— Угол \(BEC\) равен углу \(AEM\) (вертикальные углы).
— Угол \(CAD\) равен углу \(BCA\) (накрестлежащие углы при параллельных прямых \(AD\) и \(BC\)).
— Сторона \(AE = EC\) (по условию).
Следовательно, треугольники \(AEM\) и \(BEC\) равны по стороне и двум прилежащим углам.
Из равенства треугольников следует, что \(AM = BC = 5\) см.
6) Найдем длину отрезка \(MD\):
\(MD = AD — AM = 17 — 5 = 12\) см.
7) Рассмотрим треугольник \(BDM\). Его площадь можно найти по формуле:
\(S_{BDM} = \frac{1}{2} \cdot MD \cdot BH\).
Подставим известные значения:
\(S_{BDM} = \frac{1}{2} \cdot 12 \cdot 8 = 48\) см².
Ответ: \(48\) см².
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!