
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 521 Атанасян — Подробные Ответы
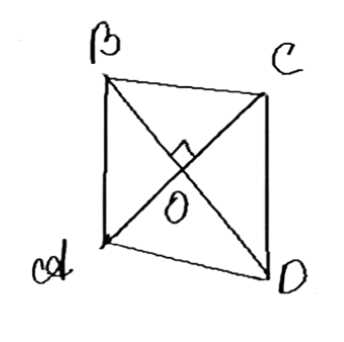
Докажите, что если диагонали четырёхугольника ABCD взаимно перпендикулярны, то \(AD^2 + BC^2 = AB^2 + CD^2\).
Дано: \(ABCD\) — четырехугольник; \(AC \perp BD\).
Доказать: \(AD^2 + BC^2 = AB^2 + CD^2\).
Доказательство:
1. \(AC \perp BD\), значит треугольники \(AOB\), \(BOC\), \(COD\), \(DOA\) — прямоугольные.
2. По теореме Пифагора для каждого треугольника:
— \(AD^2 = AO^2 + OD^2\)
— \(BC^2 = BO^2 + OC^2\)
— \(AB^2 = AO^2 + BO^2\)
— \(CD^2 = CO^2 + OD^2\)
3. Сложим \(AD^2\) и \(BC^2\):
\(
AD^2 + BC^2 = AO^2 + OD^2 + BO^2 + OC^2
\)
4. Сгруппируем слагаемые:
\(
AD^2 + BC^2 = (AO^2 + BO^2) + (OC^2 + OD^2)
\)
5. Подставим \(AB^2\) и \(CD^2\):
\(
AD^2 + BC^2 = AB^2 + CD^2
\)
Что и требовалось доказать.
Дано: \(ABCD\) — четырехугольник; \(AC \perp BD\).
Требуется доказать: \(AD^2 + BC^2 = AB^2 + CD^2\).
Доказательство:
1) Поскольку \(AC \perp BD\), то диагонали \(AC\) и \(BD\) пересекаются под прямым углом. Обозначим точку пересечения диагоналей как \(O\).
2) Рассмотрим треугольники, образованные диагоналями:
— \(\triangle AOB\) — прямоугольный, так как \(AC \perp BD\).
— \(\triangle BOC\) — прямоугольный, так как \(AC \perp BD\).
— \(\triangle COD\) — прямоугольный, так как \(AC \perp BD\).
— \(\triangle DOA\) — прямоугольный, так как \(AC \perp BD\).
3) Применим теорему Пифагора к каждому из этих треугольников:
— Для \(\triangle AOB\): \(AB^2 = AO^2 + BO^2\).
— Для \(\triangle BOC\): \(BC^2 = BO^2 + CO^2\).
— Для \(\triangle COD\): \(CD^2 = CO^2 + DO^2\).
— Для \(\triangle DOA\): \(AD^2 = AO^2 + DO^2\).
4) Сложим равенства для \(AD^2\) и \(BC^2\):
\[AD^2 + BC^2 = (AO^2 + DO^2) + (BO^2 + CO^2).\]
5) Перегруппируем слагаемые:
\[AD^2 + BC^2 = (AO^2 + BO^2) + (CO^2 + DO^2).\]
6) Подставим выражения для \(AB^2\) и \(CD^2\) из п. 3:
\[AD^2 + BC^2 = AB^2 + CD^2.\]
Таким образом, равенство \(AD^2 + BC^2 = AB^2 + CD^2\) доказано.
Дополнительные пояснения:
— В процессе доказательства использовались свойства прямоугольных треугольников и теорема Пифагора.
— Перегруппировка слагаемых позволила связать суммы квадратов сторон четырехугольника через квадраты его диагоналей.
— Данное доказательство является универсальным и применимо к любому четырехугольнику, диагонали которого перпендикулярны.
Ответ: \(AD^2 + BC^2 = AB^2 + CD^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!