
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 520 Атанасян — Подробные Ответы
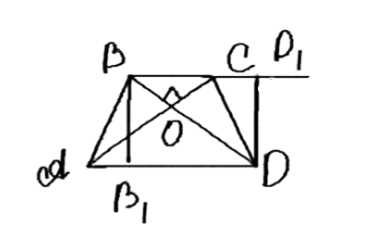
Диагонали равнобедренной трапеции взаимно перпендикулярны, а сумма оснований равна \[2a\]. Найдите площадь трапеции.
Дано: \(ABCD\) — равнобедренная трапеция; \(AC \perp BD\); \(BC + AD = 2a\).
Решение:
1) Площадь трапеции \(S_{ABCD} = \frac{1}{2} \cdot (BC + AD) \cdot BH\). По условию \(BC + AD = 2a\), следовательно \(S_{ABCD} = a \cdot BH\).
2) Проведем дополнительные построения: \(FD \parallel BF\), тогда \(HBFD\) — прямоугольник.
3) Перенесем \(AC\) параллельным переносом, получим \(HF\), значит \(AC = HF\).
4) Рассмотрим треугольники \(ABD\) и \(ACD\): \(\angle A = \angle D\), \(AB = CD\), \(AD\) — общая, следовательно \(\triangle ABD = \triangle ACD\) (по двум сторонам и углу между ними). Отсюда \(AC = BD\).
5) Рассмотрим \(BHDF\): \(BH \perp HD\), \(DF \perp BF\), \(BD = HF\), \(HF \perp BD\), значит \(BHDF\) — квадрат, следовательно \(S_{BHDF} = BH^2\).
6) Площадь трапеции \(S_{ABCD} = S_{BHDF} = BH^2\).
7) Из \(S_{ABCD} = a \cdot BH\) и \(S_{ABCD} = BH^2\) следует \(a = BH\).
8) Таким образом, \(S_{ABCD} = a^2\).
Ответ: \(S_{ABCD} = a^2\).
Дано: \(ABCD\) — равнобедренная трапеция; \(AC \perp BD\); \(BC + AD = 2a\).
Решение:
1) Площадь трапеции \(S_{ABCD}\) вычисляется по формуле:
\[S_{ABCD} = \frac{1}{2} \cdot (BC + AD) \cdot BH.\]
По условию \(BC + AD = 2a\), следовательно:
\[S_{ABCD} = \frac{1}{2} \cdot 2a \cdot BH = a \cdot BH.\]
2) Проведем дополнительные построения. Поскольку \(ABCD\) — равнобедренная трапеция, её боковые стороны \(AB\) и \(CD\) равны, а основания \(AD\) и \(BC\) параллельны. Проведем высоту \(BH\) из вершины \(B\) на основание \(AD\).
3) Построим прямую \(FD\), параллельную \(BF\). Так как \(BF\) является диагональю трапеции, а \(FD\) параллельна \(BF\), то четырехугольник \(HBFD\) будет прямоугольником.
4) Перенесем диагональ \(AC\) параллельным переносом так, чтобы она совпала с отрезком \(HF\). Это возможно, так как \(AC\) и \(HF\) равны по длине и параллельны. Следовательно, \(AC = HF\).
5) Рассмотрим треугольники \(ABD\) и \(ACD\). У них:
— \(\angle A = \angle D\) (по свойству равнобедренной трапеции),
— \(AB = CD\) (по определению равнобедренной трапеции),
— сторона \(AD\) общая.
Следовательно, \(\triangle ABD = \triangle ACD\) по двум сторонам и углу между ними.
6) Из равенства треугольников следует, что \(AC = BD\) (как соответствующие элементы равных фигур).
7) Рассмотрим четырехугольник \(BHDF\). У него:
— \(BH \perp HD\) (так как \(BH\) — высота),
— \(DF \perp BF\) (по построению),
— \(BD = HF\) (из п. 4),
— \(HF \perp BD\) (по условию задачи).
Таким образом, \(BHDF\) — квадрат, и его площадь равна \(S_{BHDF} = BH^2\).
8) Площадь трапеции \(ABCD\) равна площади квадрата \(BHDF\), так как они состоят из одинаковых частей. Следовательно:
\[S_{ABCD} = S_{BHDF} = BH^2.\]
9) Из п. 1 и п. 8 следует, что:
\[a \cdot BH = BH^2.\]
Отсюда:
\[BH = a.\]
10) Подставляем \(BH = a\) в формулу площади трапеции:
\[S_{ABCD} = a^2.\]
Ответ: \(S_{ABCD} = a^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!