
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 515 Атанасян — Подробные Ответы
Найдите площадь равнобедренного треугольника, если:
а) боковая сторона равна 20 см, а угол при основании равен \(30^\circ\);
б) высота, проведённая к боковой стороне, равна 6 см и образует с основанием угол в \(45^\circ\).
Дано: \(\Delta ABC\) — равнобедренный; \(AB = BC\);
а) \(AB = 20\) см; \(\angle A = 30^\circ\);
б) \(AH = 6\) см; \(\angle HAC = 45^\circ\).
Найти: \(S_{ABC}\) — ?
Решение:
а)
1) \(\Delta BMA\) — прямоугольный: \(\angle A = 30^\circ \Rightarrow BM = \frac{AB}{2} = 10\) см.
2) \(AM = AB \cdot \cos 30^\circ = 20 \cdot \frac{\sqrt{3}}{2} = 10\sqrt{3}\) см; \(AC = 2AM = 20\sqrt{3}\) см.
3) \(S_{ABC} = \frac{AC \cdot BM}{2} = \frac{20\sqrt{3} \cdot 10}{2} = 100\sqrt{3}\) см².
б)
1) \(\Delta AHC\) — прямоугольный: \(\angle C = 90^\circ — 45^\circ = 45^\circ\).
2) \(\Delta AHC\) — равнобедренный: \(HC = AH = 6\) см.
3) \(AC = \sqrt{AH^2 + HC^2} = \sqrt{36 + 36} = 6\sqrt{2}\) см.
4) \(\angle B = 90^\circ\), \(AB = AH = 6\) см.
5) \(S_{ABC} = \frac{AH \cdot HC}{2} = \frac{6 \cdot 6}{2} = 18\) см².
Ответ:
а) \(S_{ABC} = 100\sqrt{3}\) см²;
б) \(S_{ABC} = 18\) см².
Дано: \(\Delta ABC\) — равнобедренный; \(AB = BC\);
а) \(AB = 20\) см; \(\angle A = 30^\circ\);
б) \(AH = 6\) см; \(\angle HAC = 45^\circ\).
Найти: \(S_{ABC}\) — ?
Решение:
а)
1) \(\Delta BMA\) — прямоугольный (так как \(BM \perp AC\)): \(\angle A = 30^\circ \Rightarrow BM = \frac{AB}{2} = 10\) см
(по свойству прямоугольного треугольника).
2) \(AM = MC\) (так как \(BM\) — медиана в равнобедренном треугольнике), \(AC = AM + MC = 2AM\).
Найдем \(AM\):
\[
AM = AB \cdot \cos 30^\circ = 20 \cdot \frac{\sqrt{3}}{2} = 10\sqrt{3} \text{ см.}
\]
Тогда \(AC = 2 \cdot 10\sqrt{3} = 20\sqrt{3}\) см.
3) Площадь треугольника \(ABC\):
\[
S_{ABC} = \frac{AC \cdot BM}{2} = \frac{20\sqrt{3} \cdot 10}{2} = 100\sqrt{3} \text{ см}^2.
\]
б)
1) Рассмотрим \(\Delta AHC\) — прямоугольный:
\[
\angle C = 90^\circ — \angle HAC = 90^\circ — 45^\circ = 45^\circ \]
(по свойству прямоугольного треугольника)
2) \(\angle C = \angle HAC = 45^\circ \Rightarrow \Delta AHC\) — равнобедренный.
3) По теореме Пифагора:
\[
AC^2 = AH^2 + HC^2 = 6^2 + 6^2 = 36 + 36 = 72 \Rightarrow AC = 6\sqrt{2} \text{ см.}
\]
4) \(\angle C = 45^\circ\), \(AB = BC\), следовательно:
\[
\angle A = 45^\circ \Rightarrow \angle B = 90^\circ \text{ (по теореме о сумме углов в треугольнике).}
\]
Тогда \(AH\) совпадает с \(AB\), и \(AB = AH = 6\) см.
5) Площадь треугольника \(ABC\):
\[
S_{ABC} = \frac{AH \cdot HC}{2} = \frac{6 \cdot 6}{2} = 18 \text{ см}^2.
\]
Ответ:
а) \(S_{ABC} = 100\sqrt{3}\) см²;
б) \(S_{ABC} = 18\) см².
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


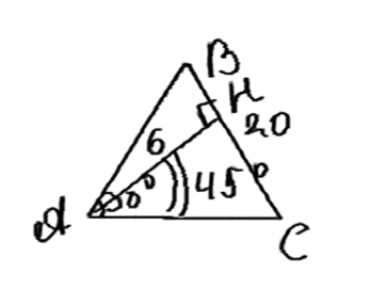

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!