
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 513 Атанасян — Подробные Ответы
Диагонали ромба равны 18 м и 24 м. Найдите периметр ромба и расстояние между параллельными сторонами.
Дано: ABCD — ромб, диагонали AC = 24 м и BD = 18 м.
Найти: периметр ромба и расстояние между параллельными сторонами.
Решение:
1. Диагонали делятся пополам: \(AO = OC = \frac{24}{2} = 12\) м, \(BO = OD = \frac{18}{2} = 9\) м.
2. В прямоугольном треугольнике \(ABO\) по теореме Пифагора: \(AB^2 = AO^2 + BO^2 = 12^2 + 9^2 = 225\), \(AB = \sqrt{225} = 15\) м.
3. Периметр ромба: \(P_{ABCD} = 4 \times 15 = 60\) м.
4. Площадь ромба: \(S_{ABCD} = \frac{24 \times 18}{2} = 216\) м².
5. Высота ромба: \(h = \frac{216}{15} = 14,4\) м.
Ответ: \(P_{ABCD} = 60\) м, \(h = 14,4\) м.
Дано: ABCD — ромб, диагонали AC = 24 м и BD = 18 м.
Необходимо найти периметр ромба и расстояние между параллельными сторонами.
Решение:
1. В ромбе диагонали пересекаются под прямым углом и делятся пополам. Это значит, что \(AO = OC = \frac{AC}{2} = \frac{24}{2} = 12\) м и \(BO = OD = \frac{BD}{2} = \frac{18}{2} = 9\) м.
2. Рассмотрим треугольник \(ABO\). Он является прямоугольным, так как диагонали ромба перпендикулярны. Для нахождения стороны ромба \(AB\) используем теорему Пифагора:
\(AB^2 = AO^2 + BO^2\)
\(AB^2 = 12^2 + 9^2 = 144 + 81 = 225\)
\(AB = \sqrt{225} = 15\) м
3. Периметр ромба равен сумме длин всех его сторон. Поскольку все стороны ромба равны, периметр \(P_{ABCD}\) можно найти по формуле:
\(P_{ABCD} = 4 \times AB = 4 \times 15 = 60\) м
4. Площадь ромба \(S_{ABCD}\) можно найти через произведение диагоналей:
\(S_{ABCD} = \frac{AC \times BD}{2} = \frac{24 \times 18}{2} = \frac{432}{2} = 216\) м²
5. Высота ромба (расстояние между параллельными сторонами) \(h\) находится через площадь и сторону ромба:
\(h = \frac{S_{ABCD}}{AB} = \frac{216}{15} = 14,4\) м
Ответ: периметр ромба \(P_{ABCD} = 60\) м, высота \(h = 14,4\) м.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


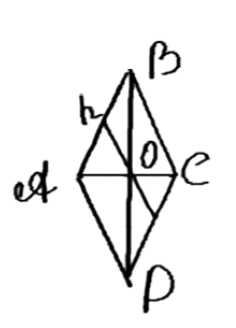

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!