Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
Ключевые особенности учебника:
1. Четкая структура:
Материал разбит на логически связанные разделы, каждый из которых посвящен отдельной теме, что облегчает восприятие и изучение.
2. Понятное изложение:
Доступный язык и стиль подачи материала делают даже сложные темы понятными для школьников.
3. Разнообразие задач:
Учебник содержит большое количество задач разной степени сложности, позволяя каждому ученику выбрать подходящие упражнения и совершенствовать свои навыки.
4. Наглядные иллюстрации:
Схемы и рисунки помогают лучше понять материал и визуализировать геометрические фигуры и их свойства.
5. Примеры из жизни:
Практические задачи, связанные с реальными ситуациями, делают изучение геометрии интересным и полезным.
6. Поддержка для учителей:
Методические рекомендации помогают преподавателям эффективно организовать уроки и использовать материал учебника.
Вывод:
Учебник Атанасяна по геометрии — это универсальный инструмент для изучения предмета, который сочетает понятность, практичность и разнообразие. Он подходит как для самостоятельного изучения, так и для работы в классе, делая процесс обучения более эффективным и увлекательным.
ГДЗ по Геометрии 8 класс Номер 512 Атанасян — Подробные Ответы
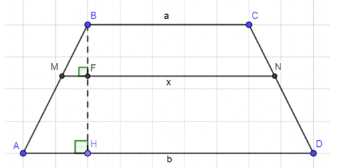
Основания трапеции равны а и b. Отрезок с концами на боковых сторонах трапеции, параллельный основаниям, разделяет трапецию на две равновеликие трапеции. Найдите длину этого отрезка.
Дано: ABCD — трапеция с основаниями BC = a и AD = b. Отрезок MN параллелен основаниям и делит трапецию на две равновеликие трапеции. Найти длину отрезка MN.
Решение: Обозначим MN = x. Площадь трапеции SAMND равна площади трапеции SMBCN. Выразим площади через высоты и основания: \[S_{AMND} = \frac{1}{2} \cdot (b + x) \cdot (BH — BF)\] и \[S_{MBCN} = \frac{1}{2} \cdot (a + x) \cdot BF\]. Поскольку площади равны, получаем уравнение: \[(b + x)(BH — BF) = (a + x) \cdot BF\]. Раскроем скобки и упростим: \[b \cdot BH + x \cdot BH — b \cdot BF — x \cdot BF = a \cdot BF + x \cdot BF\], \[b \cdot BH + x \cdot BH = a \cdot BF + x \cdot BF + x \cdot BF + b \cdot BF\], \[(b + x) \cdot BH = (a + b + 2x) \cdot BF\]. Выразим BH через BF: \[BH = \frac{(a + b + 2x) \cdot BF}{b + x}\]. Площадь всей трапеции ABCD равна сумме площадей SAMND и SMBCN: \[S_{ABCD} = S_{AMND} + S_{MBCN}\], \[\frac{1}{2} \cdot (a + b) \cdot BH = \frac{1}{2} \cdot (b + x) \cdot (BH — BF) + \frac{1}{2} \cdot (a + x) \cdot BF\]. Упростим уравнение: \[(a + b) \cdot BH = (b + x) \cdot (BH — BF) + (a + x) \cdot BF\], \[a \cdot BH + b \cdot BH = b \cdot BH — b \cdot BF + x \cdot BH — x \cdot BF + a \cdot BF + x \cdot BF\], \[a \cdot BH — x \cdot BH = a \cdot BF — b \cdot BF\], \[(a — x) \cdot BH = (a — b) \cdot BF\]. Подставим выражение для BH: \[(a — x) \cdot \frac{(a + b + 2x) \cdot BF}{b + x} = (a — b) \cdot BF\]. Упростим и решим уравнение: \[\frac{(a — x)(a + b + 2x)}{b + x} = a — b\], \[(a — x)(a + b + 2x) = (b + x)(a — b)\], \[a^2 + ab + 2ax — ax — bx — 2x^2 = ba — b^2 + ax — bx\], \[a^2 + 2ax — ax — 2x^2 + b^2 — ax = 0\], \[a^2 — 2x^2 + b^2 = 0\]. Решим уравнение относительно x: \[2x^2 = a^2 + b^2\], \[x^2 = \frac{a^2 + b^2}{2}\], \[x = \sqrt{\frac{a^2 + b^2}{2}}\]. Ответ: Длина отрезка MN равна \[\sqrt{\frac{a^2 + b^2}{2}}\].
Дано: ABCD — трапеция с основаниями BC = a и AD = b. Отрезок MN параллелен основаниям и делит трапецию на две равновеликие трапеции. Найти длину отрезка MN.
Решение:
1) Обозначим MN = x.
2) Площадь трапеции SAMND равна площади трапеции SMBCN.
3) Выразим площади через высоты и основания:
\[ S_{AMND} = \frac{1}{2} \cdot (b + x) \cdot (BH — BF) \]
\[ S_{MBCN} = \frac{1}{2} \cdot (a + x) \cdot BF \]
4) Поскольку площади равны, получаем уравнение:
\[ (b + x)(BH — BF) = (a + x) \cdot BF \]
5) Раскроем скобки и упростим:
\[ b \cdot BH + x \cdot BH — b \cdot BF — x \cdot BF = a \cdot BF + x \cdot BF \]
\[ b \cdot BH + x \cdot BH = a \cdot BF + x \cdot BF + x \cdot BF + b \cdot BF \]
\[ (b + x) \cdot BH = (a + b + 2x) \cdot BF \]
6) Выразим BH через BF:
\[ BH = \frac{(a + b + 2x) \cdot BF}{b + x} \]
7) Площадь всей трапеции ABCD равна сумме площадей SAMND и SMBCN:
\[ S_{ABCD} = S_{AMND} + S_{MBCN} \]
\[ \frac{1}{2} \cdot (a + b) \cdot BH = \frac{1}{2} \cdot (b + x) \cdot (BH — BF) + \frac{1}{2} \cdot (a + x) \cdot BF \]
8) Упростим уравнение:
\[ (a + b) \cdot BH = (b + x) \cdot (BH — BF) + (a + x) \cdot BF \]
\[ a \cdot BH + b \cdot BH = b \cdot BH — b \cdot BF + x \cdot BH — x \cdot BF + a \cdot BF + x \cdot BF \]
\[ a \cdot BH — x \cdot BH = a \cdot BF — b \cdot BF \]
\[ (a — x) \cdot BH = (a — b) \cdot BF \]
9) Подставим выражение для BH из пункта 6:
\[ (a — x) \cdot \frac{(a + b + 2x) \cdot BF}{b + x} = (a — b) \cdot BF \]
10) Упростим и решим уравнение:
\[ \frac{(a — x)(a + b + 2x)}{b + x} = a — b \]
\[ (a — x)(a + b + 2x) = (b + x)(a — b) \]
\[ a^2 + ab + 2ax — ax — bx — 2x^2 = ba — b^2 + ax — bx \]
\[ a^2 + 2ax — ax — 2x^2 + b^2 — ax = 0 \]
\[ a^2 — 2x^2 + b^2 = 0 \]
11) Решим уравнение относительно x:
\[ 2x^2 = a^2 + b^2 \]
\[ x^2 = \frac{a^2 + b^2}{2} \]
\[ x = \sqrt{\frac{a^2 + b^2}{2}} \]
Ответ: Длина отрезка MN равна \[ \sqrt{\frac{a^2 + b^2}{2}} \].
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.