ГДЗ по Геометрии 8 класс Номер 511 Атанасян — Подробные Ответы

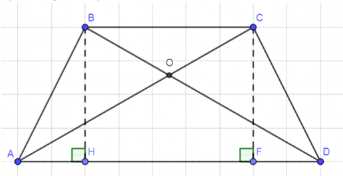
В трапеции ABCD с боковыми сторонами AB и CD диагонали пересекаются в точке О.  

а) Сравните площади треугольников ABD и ACD.  

б) Сравните площади треугольников ABO и CDO.  

в) Докажите, что выполняется равенство ОА · ОВ = ОС · OD.  

Дано: ABCD — трапеция; AC ∩ BD = O. Доказать: OA·OB = OC·OD. Сравнить: а) SABD и SACD; б) SABO и SCDO.

Решение:
а) BH = CF (как высоты): SABD = \[ \frac{1}{2} \cdot BH \cdot AD \]; SACD = \[ \frac{1}{2} \cdot CF \cdot AD \]. Так как BH = CF, то SABD = SACD.

б) SABD = SACD; SABO = SABD − SAOD; SCDO = SACD − SAOD. Следовательно, SABO = SCDO.

1) ∠BOA = ∠COD (как вертикальные);
2) По теореме об отношении площадей треугольников с равными углами: \[ \frac{SBOA}{SCOD} = \frac{BO \cdot OA}{OC \cdot OD} \];
3) Так как SABO = SCDO, то \[ \frac{BO \cdot OA}{OC \cdot OD} = 1 \]. Следовательно, OA·OB = OC·OD, что и требовалось доказать.

Ответ: а) Равны; б) Равны.

Дано: ABCD — трапеция; AC ∩ BD = O. Доказать: OA·OB = OC·OD. Сравнить: а) SABD и SACD; б) SABO и SCDO.

Решение:
а) Рассмотрим высоты BH и CF, опущенные из вершин B и C на основание AD. Поскольку ABCD — трапеция, то BH = CF. Площадь треугольника ABD вычисляется по формуле: SABD = (1/2) · BH · AD. Площадь треугольника ACD вычисляется по формуле: SACD = (1/2) · CF · AD. Так как BH = CF, то SABD = SACD.

б) Поскольку SABD = SACD, вычтем из обеих площадей площадь треугольника AOD: SABO = SABD − SAOD и SCDO = SACD − SAOD. Отсюда следует, что SABO = SCDO.

1) Углы ∠BOA и ∠COD являются вертикальными, следовательно, они равны: ∠BOA = ∠COD.
2) По теореме об отношении площадей треугольников с равными углами: (SBOA)/(SCOD) = (BO · OA)/(OC · OD).
3) Так как SABO = SCDO, то (BO · OA)/(OC · OD) = 1. Отсюда получаем: OA · OB = OC · OD, что и требовалось доказать.

Ответ: а) Площади треугольников ABD и ACD равны; б) Площади треугольников ABO и CDO равны.