
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 510 Атанасян — Подробные Ответы
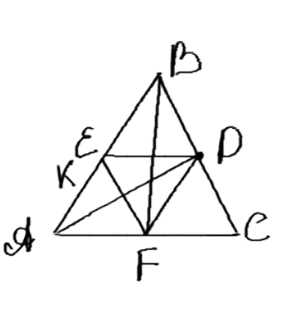
Через точку D, лежащую на стороне ВС треугольника АВС, проведены прямые, параллельные двум другим сторонам и пересекающие стороны AB и АС соответственно в точках Е и F. Докажите, что треугольники CDE и BDF равновеликие.
Дано: ΔABC; DE ∥ BC; ED ∥ AC; DF ∥ AB. Доказать: SACD = SBDF.
Доказательство: 1) EDFC — параллелограмм (FC ∥ ED, EF ∥ DC). 2) FDEB — параллелограмм (EF ∥ BD, FD ∥ EB). 3) ED — диагональ FDEB; FD — диагональ EDFC, значит SEDF = SFDEB и SEDF = SEDFC. 4) SACD = SEDFC; SBDF = SFDEB. 5) Следовательно, SACD = SBDF.
Дано: ΔABC; DE ∥ BC; ED ∥ AC; DF ∥ AB. Доказать: SACD = SBDF.
Доказательство: 1) Так как FC ∥ ED и EF ∥ DC, то EDFC — параллелограмм. 2) Так как EF ∥ BD и FD ∥ EB, то FDEB — параллелограмм. 3) ED — диагональ FDEB; FD — диагональ EDFC, следовательно: SEDF = SFDEB и SEDF = SEDFC. 4) SACD = SEDFC; SBDF = SFDEB. 5) Таким образом, SACD = SBDF, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!