Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 509 Атанасян — Подробные Ответы
Докажите, что сумма расстояний от точки, лежащей внутри равностороннего треугольника, до его сторон не зависит от положения этой точки.
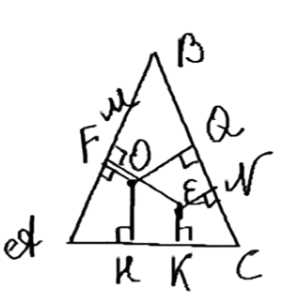
Дано: ΔABC — равносторонний треугольник, AB = BC = AC. Проведены перпендикуляры: EN ⊥ BC, OH ⊥ AC, EK ⊥ AC, OF ⊥ AB, EM ⊥ AB, OQ ⊥ BC. Доказать: EN + EK + EM = OQ + OH + OF.
Рассмотрим площади треугольников: SABC = SAEC + SBEC + SABE и SABC = SAOB + SBOC + SAOC. Подставляем: SAEC + SBEC + SABE = SAOB + SBOC + SAOC. Выразим через перпендикуляры: (1/2)*EK*AC + (1/2)*EN*BC + (1/2)*EM*AB = (1/2)*OH*AC + (1/2)*OQ*BC + (1/2)*OF*AB. Учитывая AB = BC = AC, упрощаем: (1/2)*AC*(EK + EN + EM) = (1/2)*AC*(OH + OQ + OF). Сокращаем (1/2)*AC: EK + EN + EM = OH + OQ + OF. Доказано.
Дано: ΔABC — равносторонний треугольник, где AB = BC = AC. Проведены перпендикуляры: EN ⊥ BC, OH ⊥ AC, EK ⊥ AC, OF ⊥ AB, EM ⊥ AB, OQ ⊥ BC. Требуется доказать, что EN + EK + EM = OQ + OH + OF.
Рассмотрим площади треугольников, образованных этими перпендикулярами. Площадь треугольника ABC можно выразить как сумму площадей треугольников AEC, BEC и ABE: SABC = SAEC + SBEC + SABE. Аналогично, площадь треугольника ABC также равна сумме площадей треугольников AOB, BOC и AOC: SABC = SAOB + SBOC + SAOC. Подставляем выражения для площадей: SAEC + SBEC + SABE = SAOB + SBOC + SAOC. Выразим площади через перпендикуляры: (1/2)*EK*AC + (1/2)*EN*BC + (1/2)*EM*AB = (1/2)*OH*AC + (1/2)*OQ*BC + (1/2)*OF*AB. Поскольку AB = BC = AC (по условию), упрощаем выражение: (1/2)*AC*(EK + EN + EM) = (1/2)*AC*(OH + OQ + OF). Сокращаем (1/2)*AC с обеих сторон и получаем: EK + EN + EM = OH + OQ + OF. Таким образом, EN + EK + EM = OQ + OH + OF, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.