
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 508 Атанасян — Подробные Ответы
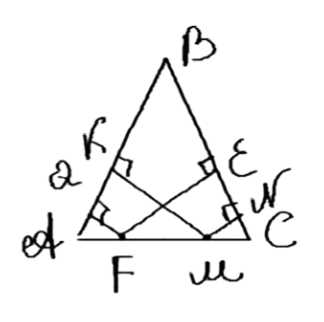
Докажите, что сумма расстояний от точки на основании равнобедренного треугольника до боковых сторон не зависит от положения этой точки.
Дано: ΔABC — равнобедренный, AB = BC. Точка M лежит на основании AC. Нужно доказать, что сумма расстояний от точки M до боковых сторон AB и BC не зависит от положения точки M.
Обозначим расстояния от точки M до сторон AB и BC как h₁ и h₂ соответственно. Площадь треугольника ABC можно выразить как SABC = (1/2)*AB*h, где h — высота треугольника, опущенная на основание AC. Площадь треугольника ABM: SABM = (1/2)*AB*h₁. Площадь треугольника CBM: SCBM = (1/2)*BC*h₂. Поскольку AB = BC, то SABM + SCBM = (1/2)*AB*(h₁ + h₂). С другой стороны, SABC = SABM + SCBM, поэтому (1/2)*AB*h = (1/2)*AB*(h₁ + h₂). Отсюда h = h₁ + h₂. Таким образом, сумма h₁ + h₂ равна высоте h и не зависит от положения точки M на основании AC.
Дано: ΔABC — равнобедренный треугольник, где AB = BC. Точка M лежит на основании AC. Требуется доказать, что сумма расстояний от точки M до боковых сторон AB и BC не зависит от положения точки M на основании AC.
Обозначим расстояния от точки M до сторон AB и BC как h₁ и h₂ соответственно. Площадь треугольника ABC можно выразить через формулу SABC = (1/2)*AB*h, где h — высота треугольника, опущенная на основание AC. Площадь треугольника ABM вычисляется как SABM = (1/2)*AB*h₁, а площадь треугольника CBM — как SCBM = (1/2)*BC*h₂. Поскольку AB = BC, сумма площадей треугольников ABM и CBM равна SABM + SCBM = (1/2)*AB*(h₁ + h₂). С другой стороны, площадь треугольника ABC равна сумме площадей треугольников ABM и CBM, то есть SABC = SABM + SCBM. Подставляя выражения для площадей, получаем (1/2)*AB*h = (1/2)*AB*(h₁ + h₂). Отсюда следует, что h = h₁ + h₂. Таким образом, сумма расстояний h₁ + h₂ равна высоте h треугольника ABC и не зависит от положения точки M на основании AC.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!