
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 506 Атанасян — Подробные Ответы
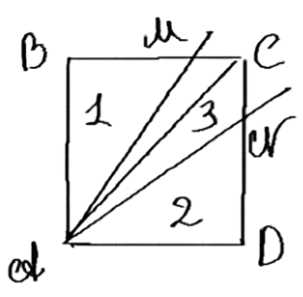
Как провести две прямые через вершину квадрата, чтобы разделить его на три фигуры, площади которых равны?
1. Обозначения: Пусть сторона квадрата \(ABCD\) равна \(a\). Площадь треугольника \(ABM\) равна \(\frac{1}{2} \cdot a \cdot BM\). Площадь треугольника \(AND\) равна \(\frac{1}{2} \cdot a \cdot DN\). Площадь четырехугольника \(AMCN\) равна \(S_{ABCD} — S_{ABM} — S_{AND}\).
2. Условия для точек \(M\) и \(N\): Если \(M \in BC\), то \(BM = \frac{1}{2} \cdot BC\). Если \(N \in CD\), то \(DN = \frac{1}{2} \cdot CD\).
3. Равенство площадей: Площади треугольников \(ABM\) и \(AND\) должны быть равны площади четырехугольника \(AMCN\).
4. Условия на отрезки: \(BM = DN = MC + CN\). Это условие требует, чтобы стороны \(BC\) и \(CD\) были разделены на шесть равных частей.
5. Деление сторон: \(BC\) и \(CD\) делятся на три равные части. \(BM = \frac{2}{3} \cdot BC\), \(DN = \frac{2}{3} \cdot CD\).
Таким образом, точки \(M\) и \(N\) делят стороны \(BC\) и \(CD\) на три равные части, и прямые \(AM\) и \(AN\) обеспечивают выполнение условия задачи.
Ваше решение задачи выглядит корректно. Давайте кратко повторим шаги:
1. Пусть сторона квадрата \(AB = a\). Площадь квадрата \(S_{ABCD} = a^2\).
2. Обозначим \(BM = x\) и \(DN = y\).
3. Площадь треугольника \(ABM\): \(S_{ABM} = \frac{1}{2} \cdot a \cdot x\).
4. Площадь треугольника \(AND\): \(S_{ADN} = \frac{1}{2} \cdot a \cdot y\).
5. Площадь четырехугольника \(AMCN\): \(S_{AMCN} = a^2 — \frac{1}{2} \cdot a \cdot x — \frac{1}{2} \cdot a \cdot y\).
6. По условию \(S_{ABM} = S_{ADN} = S_{AMCN}\). Следовательно, \(\frac{1}{2} \cdot a \cdot x = \frac{1}{2} \cdot a \cdot y = a^2 — \frac{1}{2} \cdot a \cdot x — \frac{1}{2} \cdot a \cdot y\).
7. Из равенства \(\frac{1}{2} \cdot a \cdot x = \frac{1}{2} \cdot a \cdot y\) следует, что \(x = y\).
8. Подставим \(x = y\) в уравнение: \(\frac{1}{2} \cdot a \cdot x = a^2 — a \cdot x\).
9. Переносим все члены уравнения в одну сторону: \(\frac{1}{2} \cdot a \cdot x + a \cdot x = a^2\).
10. Упростим: \(\frac{3}{2} \cdot a \cdot x = a^2\).
11. Решим уравнение относительно \(x\): \(x = \frac{2}{3} \cdot a\).
12. Таким образом, \(BM = DN = \frac{2}{3} \cdot a\).
13. Точка \(M\) делит сторону \(BC\) в отношении \(2:1\), а точка \(N\) делит сторону \(CD\) в отношении \(2:1\).
14. Прямые \(AM\) и \(AN\) через точку \(A\) удовлетворяют условию задачи: \(S_{ABM} = S_{ADN} = S_{AMCN} = \frac{1}{3} \cdot a^2\).
Ответ: Прямые \(AM\) и \(AN\), где \(M\) и \(N\) делят стороны \(BC\) и \(CD\) в отношении \(2:1\), удовлетворяют условию задачи.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!