
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 505 Атанасян — Подробные Ответы
Докажите, что из всех треугольников, у которых одна сторона равна а, а другая — b, наибольшую площадь имеет тот, у которого эти стороны перпендикулярны.
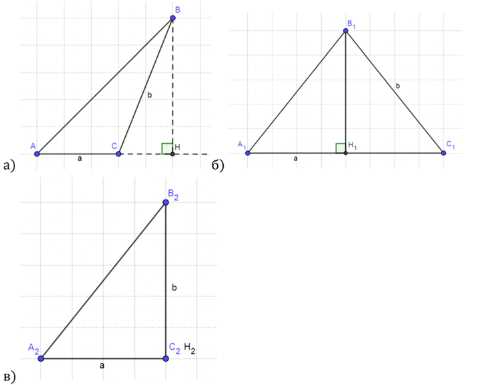
Даны три треугольника: \(ABC\), \(A_1B_1C_1\) и \(A_2B_2C_2\) с основанием \(a\) и высотами \(BH\), \(B_1H_1\) и \(b\).
В случаях а и б высоты \(BH\) и \(B_1H_1\) меньше стороны \(b\), поскольку в прямоугольном треугольнике гипотенуза всегда больше любого катета: \(b = \sqrt{a^2 + h^2}\), где \(h\) — высота, и очевидно, что \(b > h\).
Площади треугольников:
— \(S_{ABC} = \frac{1}{2} \cdot a \cdot BH\)
— \(S_{A_1B_1C_1} = \frac{1}{2} \cdot a \cdot B_1H_1\)
— \(S_{A_2B_2C_2} = \frac{1}{2} \cdot a \cdot b\)
Так как \(BH < b\) и \(B_1H_1 < b\), то площади треугольников \(ABC\) и \(A_1B_1C_1\) меньше площади треугольника \(A_2B_2C_2\): \(\frac{1}{2} \cdot a \cdot BH < \frac{1}{2} \cdot a \cdot B_1H_1 < \frac{1}{2} \cdot a \cdot b\). Таким образом, площадь треугольника \(A_2B_2C_2\) является наибольшей.
Даны три треугольника: \(ABC\), \(A_1B_1C_1\) и \(A_2B_2C_2\) с основанием \(a\) и высотами \(BH\), \(B_1H_1\) и \(b\).
В случаях а и б высоты \(BH\) и \(B_1H_1\) меньше стороны \(b\), так как в прямоугольном треугольнике гипотенуза всегда больше любого катета: \(b = \sqrt{a^2 + h^2}\), где \(h\) — высота, и очевидно, что \(b > h\).
Площади треугольников вычисляются по формуле: \(S = \frac{1}{2} \cdot \text{основание} \cdot \text{высота}\). Таким образом, для каждого треугольника получаем:
— \(S_{ABC} = \frac{1}{2} \cdot a \cdot BH\)
— \(S_{A_1B_1C_1} = \frac{1}{2} \cdot a \cdot B_1H_1\)
— \(S_{A_2B_2C_2} = \frac{1}{2} \cdot a \cdot b\)
Поскольку \(BH < b\) и \(B_1H_1 < b\), то площади треугольников \(ABC\) и \(A_1B_1C_1\) будут меньше площади треугольника \(A_2B_2C_2\). Это можно записать в виде неравенства: \( \frac{1}{2} \cdot a \cdot BH < \frac{1}{2} \cdot a \cdot B_1H_1 < \frac{1}{2} \cdot a \cdot b \) Таким образом, площадь треугольника \(A_2B_2C_2\) является наибольшей. Это подтверждает, что при фиксированном основании площадь треугольника максимальна, когда высота равна длине стороны \(b\), что соответствует случаю в.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!