ГДЗ по Геометрии 8 класс Номер 500 Атанасян — Подробные Ответы

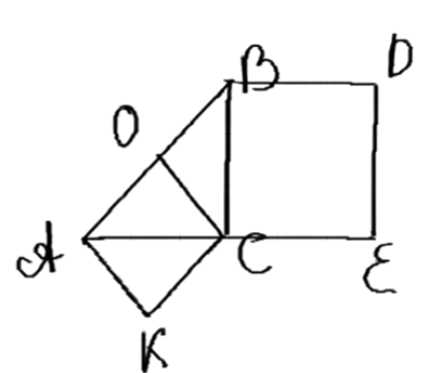
Докажите, что площадь квадрата, построенного на катете равнобедренного прямоугольного треугольника, вдвое больше площади квадрата, построенного на высоте, проведённой к гипотенузе.

Дано: \( \triangle ABC \), \( \angle C = 90^\circ \), \( AC = BC \), \( BDEC \) и \( AOCK \) — квадраты.
Доказать: \( S_{BDEC} = 2S_{AOCK} \).

Решение:
1. Пусть \( AC = BC = a \). Тогда \( S_{BDEC} = a^2 \).
2. В \( \triangle BCA \) по теореме Пифагора: \( AB^2 = a^2 + a^2 = 2a^2 \Rightarrow AB = a\sqrt{2} \).
3. Медиана \( CO \) делит \( AB \) пополам: \( AO = OB = \frac{a\sqrt{2}}{2} \).
4. В \( \triangle AOC \) по теореме Пифагора: \( OC^2 = a^2 — \left( \frac{a\sqrt{2}}{2} \right)^2 = \frac{a^2}{2} \Rightarrow OC = \frac{a}{\sqrt{2}} \).
5. Площадь квадрата \( AOCK \): \( S_{AOCK} = \left( \frac{a}{\sqrt{2}} \right)^2 = \frac{a^2}{2} \).
6. Сравниваем площади: \( S_{BDEC} = a^2 \), \( S_{AOCK} = \frac{a^2}{2} \Rightarrow S_{BDEC} = 2S_{AOCK} \).

Доказано.

Дано: треугольник \( \triangle ABC \), где \( \angle C = 90^\circ \), \( AC = BC \), \( BDEC \) и \( AOCK \) — квадраты.
Требуется доказать: \( S_{BDEC} = 2S_{AOCK} \).

Полное решение с детализацией:
1. Пусть \( AC = BC = a \). Так как \( BDEC \) — квадрат, построенный на стороне \( BC \), его площадь равна квадрату длины стороны:
\( S_{BDEC} = BC^2 = a^2. \)

2. Рассмотрим \( \triangle BCA \). По теореме Пифагора найдем длину гипотенузы \( AB \):
\( AB^2 = AC^2 + BC^2 = a^2 + a^2 = 2a^2 \Rightarrow AB = a\sqrt{2}. \)

3. Медиана \( CO \) в прямоугольном треугольнике \( \triangle BCA \) делит гипотенузу \( AB \) пополам:
\( AO = OB = \frac{AB}{2} = \frac{a\sqrt{2}}{2}. \)

4. Найдем длину отрезка \( OC \) в \( \triangle AOC \) по теореме Пифагора:
\( AC^2 = AO^2 + OC^2 \Rightarrow OC^2 = AC^2 — AO^2. \)
Подставим значения:
\( OC^2 = a^2 — \left( \frac{a\sqrt{2}}{2} \right)^2 = a^2 — \frac{2a^2}{4} = a^2 — \frac{a^2}{2} = \frac{a^2}{2}. \)
Следовательно:
\( OC = \frac{a}{\sqrt{2}}. \)

5. Квадрат \( AOCK \) построен на стороне \( OC \), поэтому его площадь равна:
\( S_{AOCK} = OC^2 = \left( \frac{a}{\sqrt{2}} \right)^2 = \frac{a^2}{2}. \)

6. Сравним площади квадратов:
\( S_{BDEC} = a^2, \quad S_{AOCK} = \frac{a^2}{2}. \)
Отсюда:
\( S_{BDEC} = 2S_{AOCK}. \)

Доказательство завершено.