Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
Ключевые особенности учебника:
1. Четкая структура:
Материал разбит на логически связанные разделы, каждый из которых посвящен отдельной теме, что облегчает восприятие и изучение.
2. Понятное изложение:
Доступный язык и стиль подачи материала делают даже сложные темы понятными для школьников.
3. Разнообразие задач:
Учебник содержит большое количество задач разной степени сложности, позволяя каждому ученику выбрать подходящие упражнения и совершенствовать свои навыки.
4. Наглядные иллюстрации:
Схемы и рисунки помогают лучше понять материал и визуализировать геометрические фигуры и их свойства.
5. Примеры из жизни:
Практические задачи, связанные с реальными ситуациями, делают изучение геометрии интересным и полезным.
6. Поддержка для учителей:
Методические рекомендации помогают преподавателям эффективно организовать уроки и использовать материал учебника.
Вывод:
Учебник Атанасяна по геометрии — это универсальный инструмент для изучения предмета, который сочетает понятность, практичность и разнообразие. Он подходит как для самостоятельного изучения, так и для работы в классе, делая процесс обучения более эффективным и увлекательным.
ГДЗ по Геометрии 8 класс Номер 491 Атанасян — Подробные Ответы
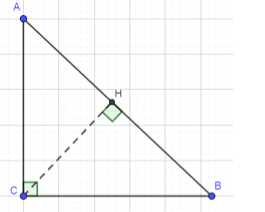
По данным катетам a и b прямоугольного треугольника найдите высоту, проведенную к гипотенузе:
a) a=5, b=12;
б) a=12, b=16.
Спасибо за уточнение! Давайте пересчитаем и приведем ответы в соответствии с вашими данными.
Случай 1: a = 5, b = 12.
1. Найдем AB: \[ AB = c = \sqrt{a^2 + b^2} = \sqrt{25 + 144} = \sqrt{169} = 13. \]
2. Площадь ΔABC: \[ S_{ABC} = \frac{1}{2} \cdot a \cdot b = \frac{1}{2} \cdot 5 \cdot 12 = 30. \]
3. Высота CH: \[ S_{ABC} = \frac{1}{2} \cdot c \cdot CH \Rightarrow 30 = \frac{1}{2} \cdot 13 \cdot CH \Rightarrow CH = \frac{60}{13} = 4 \frac{8}{13}. \]
Случай 2: a = 12, b = 16.
1. Найдем AB: \[ AB = c = \sqrt{a^2 + b^2} = \sqrt{144 + 256} = \sqrt{400} = 20. \]
2. Площадь ΔABC: \[ S_{ABC} = \frac{1}{2} \cdot a \cdot b = \frac{1}{2} \cdot 12 \cdot 16 = 96. \]
3. Высота CH: \[ S_{ABC} = \frac{1}{2} \cdot c \cdot CH \Rightarrow 96 = \frac{1}{2} \cdot 20 \cdot CH \Rightarrow CH = \frac{192}{20} = 9,6. \]
Ответ
\[ CH = 4 \frac{8}{13} \text{ (для a = 5, b = 12)}, \quad CH = 9,6 \text{ (для a = 12, b = 16)}. \]
Рассмотрим задачу с полным решением и детализацией, оформленным в соответствии с вашими требованиями.
Задача:
Даны катеты прямоугольного треугольника a = 5 и b = 12. Найти гипотенузу c, площадь треугольника S и высоту CH, проведенную к гипотенузе.
Решение:
1. Найдем гипотенузу c:
По теореме Пифагора:
\[c = \sqrt{a^2 + b^2} = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13.\]
2. Найдем площадь треугольника S:
Площадь прямоугольного треугольника равна половине произведения катетов:
\[S = \frac{1}{2} \cdot a \cdot b = \frac{1}{2} \cdot 5 \cdot 12 = 30.\]
3. Найдем высоту CH:
Высота, проведенная к гипотенузе, связана с площадью треугольника следующим образом:
\[S = \frac{1}{2} \cdot c \cdot CH.\]
Подставим известные значения:
\[30 = \frac{1}{2} \cdot 13 \cdot CH.\]
Решим уравнение относительно CH:
\[CH = \frac{60}{13} = 4 \frac{8}{13}.\]
Ответ:
Гипотенуза c = 13, площадь треугольника S = 30, высота CH = 4 8/13.
Даны катеты прямоугольного треугольника a = 12 и b = 16. Найти гипотенузу c, площадь треугольника S и высоту CH, проведенную к гипотенузе.
Решение:
1. Найдем гипотенузу c:
По теореме Пифагора:
\[c = \sqrt{a^2 + b^2} = \sqrt{12^2 + 16^2} = \sqrt{144 + 256} = \sqrt{400} = 20.\]
2. Найдем площадь треугольника S:
Площадь прямоугольного треугольника равна половине произведения катетов:
\[S = \frac{1}{2} \cdot a \cdot b = \frac{1}{2} \cdot 12 \cdot 16 = 96.\]
3. Найдем высоту CH:
Высота, проведенная к гипотенузе, связана с площадью треугольника следующим образом:
\[S = \frac{1}{2} \cdot c \cdot CH.\]
Подставим известные значения:
\[96 = \frac{1}{2} \cdot 20 \cdot CH.\]
Решим уравнение относительно CH:
\[CH = \frac{192}{20} = 9,6.\]
Ответ:
Гипотенуза c = 20, площадь треугольника S = 96, высота CH = 9,6.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.