
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 490 Атанасян — Подробные Ответы
Найдите боковую сторону и площадь равнобедренного треугольника, если:
a) основание равно 12 см, а высота, проведенная к основанию, равна 8 см;
б) основание равно 18 см, а угол, противолежащий основанию, равен 120°;
в) треугольник прямоугольный и высота, проведенная к гипотенузе, равна 7 см.
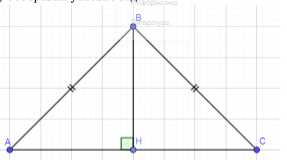
Дано: ΔABC — равнобедренный треугольник, AB = BC. Найти: AB и площадь SABC.
а) AC = 12 см; BH = 8 см.
1. SABC = (1/2) * AC * BH = (1/2) * 12 * 8 = 48 см².
2. AH = HC = AC/2 = 12/2 = 6 см.
3. AB² = BH² + AH² = 8² + 6² = 64 + 36 = 100.
AB = √100 = 10 см.
б) AC = 18 см; ∠B = 120°.
1. AH = HC = AC/2 = 18/2 = 9 см.
2. ∠ABH = 60°, ∠A = 30°.
3. AB² = (AB/2)² + 9².
AB² = AB²/4 + 81.
3AB² = 324.
AB² = 108.
AB = √108 = 6√3 см.
4. SABC = (1/2) * AC * BH = (1/2) * 18 * 3√3 = 27√3 см².
в) ∠B = 90°; BH = 7 см.
1. ∠A = ∠C = 45°.
2. BH = AH = 7 см.
3. AC = AH + HC = 2 * 7 = 14 см.
4. SABC = (1/2) * AC * BH = (1/2) * 14 * 7 = 49 см².
5. AB² = BH² + AH² = 7² + 7² = 49 + 49 = 98.
AB = √98 = 7√2 см.
Ответ:
а) SABC = 48 см², AB = 10 см.
б) SABC = 27√3 см², AB = 6√3 см.
в) SABC = 49 см², AB = 7√2 см.
Дано: ΔABC — равнобедренный треугольник, AB = BC. Найти: AB и площадь SABC.
а) AC = 12 см; BH = 8 см.
1. Площадь треугольника SABC вычисляется по формуле: SABC = (1/2) * AC * BH. Подставляем значения: SABC = (1/2) * 12 * 8 = 48 см².
2. Высота BH в равнобедренном треугольнике делит основание AC пополам: AH = HC = AC/2 = 12/2 = 6 см.
3. В треугольнике ABH применяем теорему Пифагора: AB² = BH² + AH². Подставляем значения: AB² = 8² + 6² = 64 + 36 = 100. Находим AB: AB = √100 = 10 см.
б) AC = 18 см; ∠B = 120°.
1. Высота BH делит основание AC пополам: AH = HC = AC/2 = 18/2 = 9 см.
2. Угол ∠B = 120°, поэтому ∠ABH = 60°, так как BH — биссектриса. Угол ∠A = 30°.
3. В треугольнике ABH применяем теорему Пифагора: AB² = BH² + AH². Учитывая, что BH = AB/2, получаем: AB² = (AB/2)² + 9². Раскрываем уравнение: AB² = AB²/4 + 81. Умножаем обе стороны на 4: 4AB² = AB² + 324. Переносим AB² влево: 3AB² = 324. Находим AB²: AB² = 108. Находим AB: AB = √108 = 6√3 см.
4. Площадь треугольника SABC вычисляется по формуле: SABC = (1/2) * AC * BH. Подставляем значения: SABC = (1/2) * 18 * 3√3 = 27√3 см².
в) ∠B = 90°; BH = 7 см.
1. В равнобедренном треугольнике с прямым углом ∠B углы ∠A и ∠C равны 45°.
2. Высота BH делит основание AC пополам: AH = HC = BH = 7 см.
3. Основание AC: AC = AH + HC = 2 * 7 = 14 см.
4. Площадь треугольника SABC вычисляется по формуле: SABC = (1/2) * AC * BH. Подставляем значения: SABC = (1/2) * 14 * 7 = 49 см².
5. В треугольнике ABH применяем теорему Пифагора: AB² = BH² + AH². Подставляем значения: AB² = 7² + 7² = 49 + 49 = 98. Находим AB: AB = √98 = 7√2 см.
Ответ:
а) SABC = 48 см², AB = 10 см.
б) SABC = 27√3 см², AB = 6√3 см.
в) SABC = 49 см², AB = 7√2 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!