Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 485 Атанасян — Подробные Ответы
Найдите катет прямоугольного треугольника, лежащий против угла 60°, если гипотенуза равна c.
Искомый катет b прямоугольного треугольника ABC с углом A = 60° и гипотенузой c равен:
\[b = \frac{c \cdot \sqrt{3}}{2}\]
Где c — известная гипотенуза треугольника.
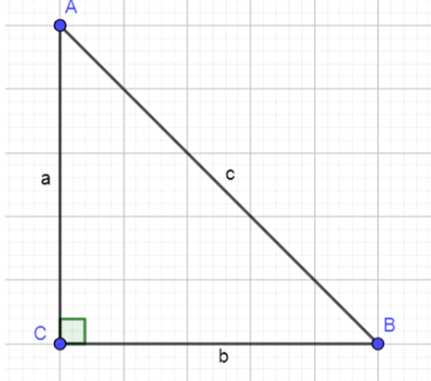
Дано: прямоугольный треугольник ABC, где угол A = 60°, гипотенуза c.
Требуется найти катет b, лежащий против угла 60°.
Согласно теореме синусов для прямоугольных треугольников, справедливо соотношение:
\[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}\]
Поскольку треугольник прямоугольный, то угол B = 90°, следовательно, \[\sin B = 1\].
Подставляя известные значения, получаем:
\[\frac{a}{\sin 60°} = \frac{b}{1} = \frac{c}{\sin 90°}\]
Упрощая выражение, имеем:
\[a = c \cdot \sin 60°\]
Учитывая, что \[\sin 60° = \frac{\sqrt{3}}{2}\], окончательно получаем:
\[b = c \cdot \frac{\sqrt{3}}{2}\]
Ответ: \[b = c \cdot \frac{\sqrt{3}}{2}\]
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.