
Учебник по геометрии для 7-9 классов под авторством Атанасяна является ценным ресурсом для школьников и учителей. Он предлагает четкую и последовательную систему изучения геометрии, способствующую развитию логического мышления и пространственного воображения.
ГДЗ по Геометрии 8 класс Номер 478 Атанасян — Подробные Ответы
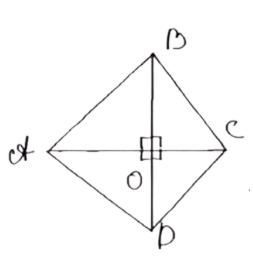
В выпуклом четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что площадь четырёхугольника равна половине произведения его диагоналей.
Дано: ABCD — выпуклый четырехугольник, диагонали AC и BD пересекаются под прямым углом. Требуется доказать, что площадь четырехугольника равна половине произведения диагоналей:
\[ S_{ABCD} = \frac{1}{2} \cdot AC \cdot BD \]
Площадь четырехугольника ABCD можно представить как сумму площадей четырех треугольников:
\[ S_{ABCD} = S_{ABO} + S_{BOC} + S_{COD} + S_{AOD} \]
Площадь каждого треугольника выражается через формулу:
\[ S = \frac{1}{2} \cdot основание \cdot высота \]
Для каждого из треугольников:
\[ S_{ABO} = \frac{1}{2} \cdot AO \cdot BO \]
\[ S_{BOC} = \frac{1}{2} \cdot BO \cdot OC \]
\[ S_{COD} = \frac{1}{2} \cdot OC \cdot OD \]
\[ S_{AOD} = \frac{1}{2} \cdot OD \cdot AO \]
Суммируем площади:
\[ S_{ABCD} = \frac{1}{2} \cdot AO \cdot BO + \frac{1}{2} \cdot BO \cdot OC + \frac{1}{2} \cdot OC \cdot OD + \frac{1}{2} \cdot OD \cdot AO \]
Группируем:
\[ S_{ABCD} = \frac{1}{2} \cdot AO \cdot (BO + OD) + \frac{1}{2} \cdot OC \cdot (BO + OD) \]
Выносим общий множитель:
\[ S_{ABCD} = \frac{1}{2} \cdot (AO + OC) \cdot BD \]
Так как AO + OC = AC, то:
\[ S_{ABCD} = \frac{1}{2} \cdot AC \cdot BD \]
Доказано.
Дано: ABCD — выпуклый четырехугольник (ромб), диагонали AC и BD пересекаются под прямым углом. Требуется доказать, что площадь ромба равна половине произведения его диагоналей:
\[ S_{ABCD} = \frac{1}{2} \cdot AC \cdot BD \]
Шаг 1. Разбиение ромба на четыре треугольника.
Диагонали AC и BD пересекаются в точке O, деля ромб на четыре треугольника: ABO, BCO, CDO и DAO. Площадь ромба равна сумме площадей этих четырех треугольников:
\[ S_{ABCD} = S_{ABO} + S_{BOC} + S_{COD} + S_{AOD} \]
Шаг 2. Формула площади треугольника.
Площадь каждого треугольника можно выразить через полупроизведение его основания и высоты. Для треугольника ABO:
\[ S_{ABO} = \frac{1}{2} \cdot AO \cdot BO \]
Для треугольника BCO:
\[ S_{BOC} = \frac{1}{2} \cdot BO \cdot OC \]
Для треугольника CDO:
\[ S_{COD} = \frac{1}{2} \cdot OC \cdot OD \]
Для треугольника AOD:
\[ S_{AOD} = \frac{1}{2} \cdot OD \cdot AO \]
Шаг 3. Суммирование площадей.
Складываем площади всех четырех треугольников:
\[ S_{ABCD} = \frac{1}{2} \cdot AO \cdot BO + \frac{1}{2} \cdot BO \cdot OC + \frac{1}{2} \cdot OC \cdot OD + \frac{1}{2} \cdot OD \cdot AO \]
Шаг 4. Группировка слагаемых.
Сгруппируем выражения следующим образом:
\[ S_{ABCD} = \frac{1}{2} \cdot AO \cdot (BO + OD) + \frac{1}{2} \cdot OC \cdot (BO + OD) \]
Шаг 5. Вынесение общего множителя.
Выносим общий множитель (BO + OD):
\[ S_{ABCD} = \frac{1}{2} \cdot (AO + OC) \cdot BD \]
Шаг 6. Замена суммы AO + OC.
Замечаем, что AO + OC равно AC, так как AC — это диагональ ромба. Подставляем это в выражение:
\[ S_{ABCD} = \frac{1}{2} \cdot AC \cdot BD \]
Вывод: Площадь ромба равна половине произведения его диагоналей. Доказано.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!